Difference between revisions of "Manuals/calci/NORMSINV"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''NORMSINV( | + | <div style="font-size:30px">'''NORMSINV (Probability)'''</div><br/> |
| − | *<math> | + | *<math>Probability</math> is the value of the Probability. |
==Description== | ==Description== | ||
*This function gives the inverse of the Standard Normal Cumulative Distribution. | *This function gives the inverse of the Standard Normal Cumulative Distribution. | ||
*In Normal Distribution formula, when the Mean is zero and the Standard Deviation is 1 then it is called Standard Normal Distribution. | *In Normal Distribution formula, when the Mean is zero and the Standard Deviation is 1 then it is called Standard Normal Distribution. | ||
| − | *If <math> NORMSDIST( | + | *If <math> NORMSDIST (Number,Accuracy)=Probability</math>, then <math>NORMSINV (Probability)=Number</math>. |
| − | *<math>NORMSINV</math> using the iterating method to find the value of <math> | + | *<math>NORMSINV</math> using the iterating method to find the value of <math>Number</math>. |
*Suppose the iteration has not converged after 100 searches, then the function gives the error result. | *Suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
| − | *In <math>NORMSINV( | + | *In <math>NORMSINV (Probability)</math>, where <math>Probability</math> is the probability value of the Standard Normal Cumulative Distribution. |
*This function will return the result as error when | *This function will return the result as error when | ||
| − | 1.<math> | + | 1.<math>Probability</math> is non-numeric. |
| − | 2.<math> | + | 2.<math>Probability<0</math> or <math>Probability>1</math>. |
==Examples== | ==Examples== | ||
Revision as of 17:19, 14 June 2018
NORMSINV (Probability)
- is the value of the Probability.
Description
- This function gives the inverse of the Standard Normal Cumulative Distribution.
- In Normal Distribution formula, when the Mean is zero and the Standard Deviation is 1 then it is called Standard Normal Distribution.
- If , then .
- using the iterating method to find the value of .
- Suppose the iteration has not converged after 100 searches, then the function gives the error result.
- In , where is the probability value of the Standard Normal Cumulative Distribution.
- This function will return the result as error when
1. is non-numeric. 2. or .
Examples
- =NORMSINV(0.9999975333) = 4.567600
- =NORMSINV(0.00241) = -2.818823592
- =NORMSINV(1) = Null
- =NORMSINV(0.00001) = -4.264890794
Related Videos
See Also
References
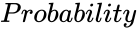 is the value of the Probability.
is the value of the Probability. , then
, then 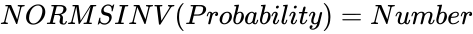 .
.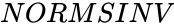 using the iterating method to find the value of
using the iterating method to find the value of 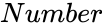 .
.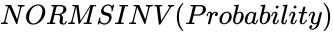 , where
, where 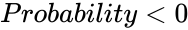 or
or 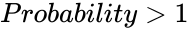 .
.