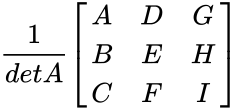Difference between revisions of "Manuals/calci/MATRIXINVERSE"
Jump to navigation
Jump to search
| Line 13: | Line 13: | ||
a & b \\ | a & b \\ | ||
c & d | c & d | ||
| − | \end{bmatrix}}^{-1}</math>=<math>1 | + | \end{bmatrix}}^{-1}</math>=<math>\frac{1}{det A }\begin{bmatrix} |
d & -b \\ | d & -b \\ | ||
-c & a | -c & a | ||
| − | \end{bmatrix}</math> = | + | \end{bmatrix}</math> =\frac{1}{ad-bc} \begin{bmatrix} |
d & -b \\ | d & -b \\ | ||
-c & a | -c & a | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
| + | *Consider 3x3 matrix A and its inverse is calculated by | ||
| + | <math>A^{-1}={\begin{bmatrix} | ||
| + | a & b & c \\ | ||
| + | d & e & f \\ | ||
| + | g & h & i | ||
| + | \end{bmatrix}}^{-1}</math>=<math>\frac{1}{det A }{\begin{bmatrix} | ||
| + | A & B & C \\ | ||
| + | D & E & F \\ | ||
| + | G & H & I | ||
| + | \end{bmatrix}}^T </math>= <math>\frac{1}{det A } {\begin{bmatrix} | ||
| + | A & D & G \\ | ||
| + | B & E & H \\ | ||
| + | C & F & I | ||
| + | \end{bmatrix}}</math> | ||
Revision as of 16:12, 20 June 2017
MATRIXINVERSE (a)
- is any matrix.
Description
- This function shows the inverse value of the given matrix.
- In , is any square matrix.
- Inverse of a square matrix is also called reciprocal of a matrix and it is denoted by .
- Consider the square matrix A has an inverse which should satisfies the following condition
- Also (Identity matrix).
- Consider 2x2 matrix:A=[a b;c d].
- The inverse of matrix A is calculated by
= =\frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}</math>
- Consider 3x3 matrix A and its inverse is calculated by
==
 is any matrix.
is any matrix.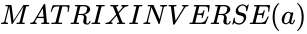 ,
, 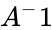 .
.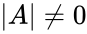
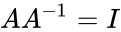 (Identity matrix).
(Identity matrix).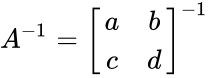 =
=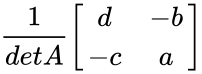 =\frac{1}{ad-bc} \begin{bmatrix}
d & -b \\
-c & a
\end{bmatrix}</math>
=\frac{1}{ad-bc} \begin{bmatrix}
d & -b \\
-c & a
\end{bmatrix}</math>
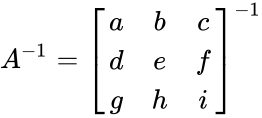 =
=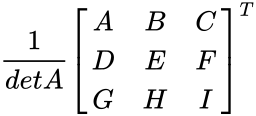 =
=