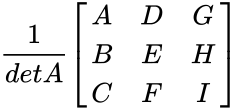Difference between revisions of "Manuals/calci/MATRIXINVERSE"
Jump to navigation
Jump to search
| Line 34: | Line 34: | ||
C & F & I | C & F & I | ||
\end{bmatrix}}</math> | \end{bmatrix}}</math> | ||
| + | where A=(ei-fh); B=-(di-fg);C=(dh-eg); D=-(bi-ch); E=(ai-cg); F=-(ah-bg); G=(bf-ce) H=-(af-cd);I=(ae-bd) | ||
Revision as of 16:17, 20 June 2017
MATRIXINVERSE (a)
- is any matrix.
Description
- This function shows the inverse value of the given matrix.
- In , is any square matrix.
- Inverse of a square matrix is also called reciprocal of a matrix and it is denoted by .
- Consider the square matrix A has an inverse which should satisfies the following condition
- Also (Identity matrix).
- Consider 2x2 matrix:A=[a b;c d].
- The inverse of matrix A is calculated by
= =\frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}</math>
- Consider 3x3 matrix A and its inverse is calculated by
==
where A=(ei-fh); B=-(di-fg);C=(dh-eg); D=-(bi-ch); E=(ai-cg); F=-(ah-bg); G=(bf-ce) H=-(af-cd);I=(ae-bd)
 is any matrix.
is any matrix.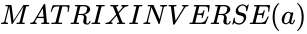 ,
, 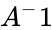 .
.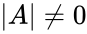
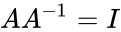 (Identity matrix).
(Identity matrix).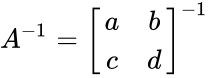 =
=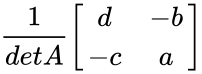 =\frac{1}{ad-bc} \begin{bmatrix}
d & -b \\
-c & a
\end{bmatrix}</math>
=\frac{1}{ad-bc} \begin{bmatrix}
d & -b \\
-c & a
\end{bmatrix}</math>
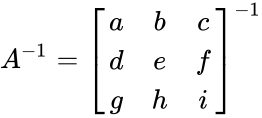 =
=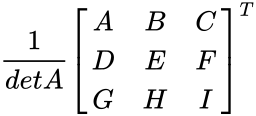 =
=