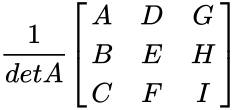Difference between revisions of "Manuals/calci/MATRIXINVERSE"
Jump to navigation
Jump to search
| Line 5: | Line 5: | ||
*This function shows the inverse value of the given matrix. | *This function shows the inverse value of the given matrix. | ||
*In <math>MATRIXINVERSE (a)</math>, <math>a</math> is any square matrix. | *In <math>MATRIXINVERSE (a)</math>, <math>a</math> is any square matrix. | ||
| − | *Inverse of a square matrix is also called reciprocal of a matrix and it is denoted by <math>A^-1</math>. | + | *Inverse of a square matrix is also called reciprocal of a matrix and it is denoted by <math>A^{-1}</math>. |
*Consider the square matrix A has an inverse which should satisfies the following condition <math>|A|\ne 0</math> | *Consider the square matrix A has an inverse which should satisfies the following condition <math>|A|\ne 0</math> | ||
*Also <math>AA^{-1}=I</math>(Identity matrix). | *Also <math>AA^{-1}=I</math>(Identity matrix). | ||
| Line 16: | Line 16: | ||
d & -b \\ | d & -b \\ | ||
-c & a | -c & a | ||
| − | \end{bmatrix}</math> =\frac{1}{ad-bc} \begin{bmatrix} | + | \end{bmatrix}</math> =<math>\frac{1}{ad-bc} \begin{bmatrix} |
d & -b \\ | d & -b \\ | ||
-c & a | -c & a | ||
Revision as of 16:19, 20 June 2017
MATRIXINVERSE (a)
- is any matrix.
Description
- This function shows the inverse value of the given matrix.
- In , is any square matrix.
- Inverse of a square matrix is also called reciprocal of a matrix and it is denoted by .
- Consider the square matrix A has an inverse which should satisfies the following condition
- Also (Identity matrix).
- Consider 2x2 matrix:A=[a b;c d].
- The inverse of matrix A is calculated by
= =
- Consider 3x3 matrix A and its inverse is calculated by
==
where A=(ei-fh); B=-(di-fg);C=(dh-eg); D=-(bi-ch); E=(ai-cg); F=-(ah-bg); G=(bf-ce) H=-(af-cd);I=(ae-bd)
 is any matrix.
is any matrix.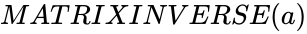 ,
, 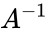 .
.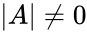
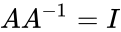 (Identity matrix).
(Identity matrix).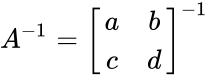 =
=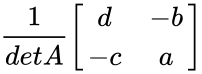 =
=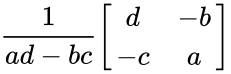
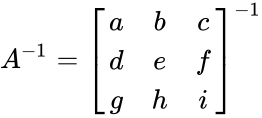 =
=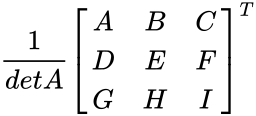 =
=