Difference between revisions of "Manuals/calci/NQUEENS"
Jump to navigation
Jump to search
2
2
3
4
| Line 39: | Line 39: | ||
2 Solutions | 2 Solutions | ||
| − | 2. NQUEENS(6) | + | *2. NQUEENS(6) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 108: | Line 108: | ||
|} | |} | ||
4 Solutions | 4 Solutions | ||
| + | |||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | *[[Manuals/calci/GENERATESUDOKU | GENERATESUDOKU ]] | ||
| + | *[[Manuals/calci/MAGICSQUARE | MAGICSQUARE ]] | ||
| + | *[[Manuals/calci/BIRTHDAYPROBABILITY | BIRTHDAYPROBABILITY ]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://www.geeksforgeeks.org/backtracking-set-3-n-queen-problem/ N Queens] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Revision as of 15:36, 26 July 2017
NQUEENS (GridSize)
- is any positive integer.
Description
- This functions creates the N-queens puzzle.
- In , is the size of the row and columns.
- Generally eight queens puzzle is the problem of placing eight chess queens on an 8x8 chessboard so that no two queens attack each other.
- Thus, a solution requires that no two queens share the same row, column or diagonal.
- The eight queens puzzle is a great example of the more general N Queens problem of placing N non attacking queens on an nxn chessboard where solutions exist for all natural numbers n with the exception of n=2 and n=3.
- This function will return the result as "0" when the value of the Grid size is 2 or 3.
- Also this will return as Error when the parameter value is non positive integer.
Examples
1. NQUEENS(4)
1| _|Q|_|_| |
| _|_|_|Q| |
| Q|_|_|_| |
| _|_|Q|_| |
| _|Q|_|_| |
| _|_|_|Q| |
| Q|_|_|_| |
| _|_|Q|_| |
2 Solutions
- 2. NQUEENS(6)
| _|Q|_|_|_|_| |
| _|_|_|Q|_|_| |
| _|_|_|_|_|Q| |
| Q|_|_|_|_|_| |
| _|_|Q|_|_|_| |
| _|_|_|_|Q|_| |
| _|_|Q|_|_|_| |
| _|_|_|_|_|Q| |
| _|Q|_|_|_|_| |
| _|_|_|_|Q|_| |
| Q|_|_|_|_|_| |
| _|_|_|Q|_|_| |
| _|_|_|Q|_|_| |
| Q|_|_|_|_|_| |
| _|_|_|_|Q|_| |
| _|Q|_|_|_|_| |
| _|_|_|_|_|Q| |
| _|_|Q|_|_|_| |
| _|_|_|_|Q|_| |
| _|_|Q|_|_|_| |
| Q|_|_|_|_|_| |
| _|_|_|_|_|Q| |
| _|_|_|Q|_|_| |
| _|Q|_|_|_|_| |
4 Solutions
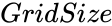 is any positive integer.
is any positive integer. ,
, 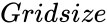 is the size of the row and columns.
is the size of the row and columns.