Difference between revisions of "Manuals/calci/IMLN"
Jump to navigation
Jump to search
(Created page with "<div id="16SpaceContent" align="left"><div class="ZEditBox" align="justify"> Syntax </div></div> ---- <div id="4SpaceContent" align="left"><div class="ZEditBox" align=...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''IMLN(z)'''</div><br/> |
| + | *<math>z</math> is the complex number is of the form <math>x+iy</math> | ||
| − | + | ==Description== | |
| + | *This function gives the natural logarithm of a complex number. | ||
| + | *In IMLN(z),Where z is the complex number in the form of "x+iy".i.e. x&y are the real numbers. | ||
| + | *'I' imaginary unit .i=sqrt(-1). | ||
| + | *A logarithm of z is a complex number w such that z = e^w and it is denoted by ln(z). | ||
| + | *If z = x+iy with x&y are real numbers then natural logarithm of a complex number : <math>ln(z)= w = ln(|z|) + iarg(z) =ln(sqrt(x^2+y^2)+itan^-1(y/x</math> adding integer multiples of 2πi gives all the others. | ||
| + | *We can use COMPLEX function to convert real and imaginary number in to a complex number. | ||
| + | ==Examples== | ||
| − | + | #IMLN("3-2i")=1.28247467873077-0.588002603547568i | |
| − | + | #IMLN("6+7i")=2.22132562824516+0.862170054667226i | |
| − | + | #IMLN("4")=1.38629436111989 But calci is not considering the zero value of imaginary value of z. | |
| + | #IMLN("10i")=2.30258509299405+1.5707963267949i | ||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/IMLOG10 | IMLOG10 ]] | ||
| + | *[[Manuals/calci/IMLOG2 | IMLOG2 ]] | ||
| + | *[[Manuals/calci/COMPLEX | COMPLEX ]] | ||
| − | |||
| − | |||
| − | |||
| − | + | ==References== | |
| − | + | [http://en.wikipedia.org/wiki/Bessel_function Bessel Function] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 03:00, 16 December 2013
IMLN(z)
- is the complex number is of the form
Description
- This function gives the natural logarithm of a complex number.
- In IMLN(z),Where z is the complex number in the form of "x+iy".i.e. x&y are the real numbers.
- 'I' imaginary unit .i=sqrt(-1).
- A logarithm of z is a complex number w such that z = e^w and it is denoted by ln(z).
- If z = x+iy with x&y are real numbers then natural logarithm of a complex number : adding integer multiples of 2πi gives all the others.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
- IMLN("3-2i")=1.28247467873077-0.588002603547568i
- IMLN("6+7i")=2.22132562824516+0.862170054667226i
- IMLN("4")=1.38629436111989 But calci is not considering the zero value of imaginary value of z.
- IMLN("10i")=2.30258509299405+1.5707963267949i
See Also
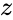 is the complex number is of the form
is the complex number is of the form 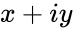
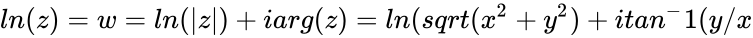 adding integer multiples of 2πi gives all the others.
adding integer multiples of 2πi gives all the others.