Difference between revisions of "Manuals/calci/PASCALTRIANGLE"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''PASCALTRIANGLE'''(level) where '''level''' is any real number </div> ---- <div id="1SpaceContent" clas...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''PASCALTRIANGLE(r)'''</div><br/> |
| + | *<math>r</math> is the row number. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the Coefficients of the Pascal triangle. | ||
| + | *In <math>PASCALTRIANGLE(r)</math> , r is the row number of the Pascal triangle. | ||
| + | *Pascal triangle is the arrangement of numbers of the Binomial coefficients in a triangular shape. | ||
| + | *It is started with the number 1 at the top in the 1st row. | ||
| + | *Then from the 2nd row each number in the triangle is the sum of the two directly above it. | ||
| + | *The construction is related to the binomial coefficients by Pascal's rule is : | ||
| + | <math>(x+y)^n=\sum_{k=0}^n \binom{n}{k}x^{n-k} .y^k </math>. where \binom{n}{k} is the binomial coefficient. | ||
| + | *This function will return the result as error when the r \le 0. | ||
| + | |||
| + | ==Examples== | ||
| + | PASCALTRIANGLE(1)=1 | ||
| + | PASCALTRIANGLE(2)=1 | ||
| + | 1 1 | ||
| + | |||
| + | PASCALTRIANGLE(3)=1 | ||
| + | 1 1 | ||
| + | 1 2 1 | ||
| + | |||
| + | PASCALTRIANGLE(0)=NULL | ||
| + | |||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | ==References== | ||
| + | * [http://www.mathsisfun.com/pascals-triangle.html Pascal's Triangle ] | ||
| + | |||
'''PASCALTRIANGLE'''(level) | '''PASCALTRIANGLE'''(level) | ||
| Line 31: | Line 60: | ||
Lets see an example in (Column2Row1) | Lets see an example in (Column2Row1) | ||
| − | + | UNIQ9eec20026ff870ff-nowiki-00000002-QINU | |
Returns 1,1,1,1,2,1 for PASCALTRIANGLE(3) | Returns 1,1,1,1,2,1 for PASCALTRIANGLE(3) | ||
Revision as of 22:48, 5 January 2014
PASCALTRIANGLE(r)
- is the row number.
Description
- This function gives the Coefficients of the Pascal triangle.
- In , r is the row number of the Pascal triangle.
- Pascal triangle is the arrangement of numbers of the Binomial coefficients in a triangular shape.
- It is started with the number 1 at the top in the 1st row.
- Then from the 2nd row each number in the triangle is the sum of the two directly above it.
- The construction is related to the binomial coefficients by Pascal's rule is :
. where \binom{n}{k} is the binomial coefficient.
- This function will return the result as error when the r \le 0.
Examples
PASCALTRIANGLE(1)=1 PASCALTRIANGLE(2)=1
1 1
PASCALTRIANGLE(3)=1
1 1
1 2 1
PASCALTRIANGLE(0)=NULL
See Also
References
PASCALTRIANGLE(level)
where
level is any real number
PASCALTRIANGLE function returns pascal's triangle for the given level.
PASCALTRIANGLE returns NaN if level is not a real number.
PASCALTRIANGLE
Lets see an example in (Column2Row1)
?UNIQ9eec20026ff870ff-nowiki-00000002-QINU?
Returns 1,1,1,1,2,1 for PASCALTRIANGLE(3)
Syntax
Remarks
Examples
Description
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 3 | 1,1,1,1,2,1 | ||
| Row2 | ||||
| Row3 | ||||
| Row4 | ||||
| Row5 | ||||
| Row6 |
| File:Calci1.gif | $ |
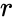 is the row number.
is the row number. , r is the row number of the Pascal triangle.
, r is the row number of the Pascal triangle.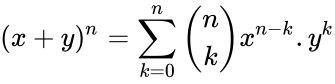 . where \binom{n}{k} is the binomial coefficient.
. where \binom{n}{k} is the binomial coefficient.