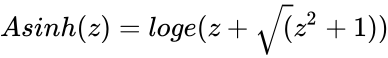Difference between revisions of "Manuals/calci/ASINH"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*Here 'z' is any real number. | *Here 'z' is any real number. | ||
*Inverse Hyperbolic Sine of a number is defined by <math> Asinh(z) = loge(z +\sqrt(z^2 + 1))</math> | *Inverse Hyperbolic Sine of a number is defined by <math> Asinh(z) = loge(z +\sqrt(z^2 + 1))</math> | ||
| − | *ASINH(-z)=-ASINH(z) | + | *ASINH(-z) = -ASINH(z) |
== Examples == | == Examples == | ||
Revision as of 22:31, 5 November 2013
ASINH(z)
- where z is any real number
Description
- This function gives the Inverse Hyperbolic Sine of a number.
- Here 'z' is any real number.
- Inverse Hyperbolic Sine of a number is defined by
- ASINH(-z) = -ASINH(z)
Examples
ASINH(z)
- z is any real number.
| ASINH(z) | Value(Radian) |
| ASINH(2) | 1.44363547517881 |
| ASINH(45) | 4.499933104264103 |
| ASINH(-90) | -5.192987713658952 |