Difference between revisions of "Manuals/calci/COMBIN"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
*If order is a matter it is a Permutation. | *If order is a matter it is a Permutation. | ||
*A combination is denoted by nCr or <math>\binom{n}{r}</math>. | *A combination is denoted by nCr or <math>\binom{n}{r}</math>. | ||
| − | *A formula for the number of possible combinations of R objects from a set of N objects is <math>\binom{n}{r}=\frac{n!}{r!(n-r)!}</math> where n!=1*2*3*...*n& r< | + | *A formula for the number of possible combinations of R objects from a set of N objects is <math>\binom{n}{r}=\frac{n!}{r!(n-r)!}</math> where <math>n!=1*2*3*...*n </math>& <math>r \le n</math>. |
| − | *This function will give | + | *This function will give Error Result when |
| − | * | + | **The N&R are non numeric |
| − | * | + | **The N&R < 0 or N < R |
| − | *When we are giving the N&R values in decimals ,it will convert in to Integers. | + | *When we are giving the N&R values in decimals, it will automatically convert in to Integers. |
*For e.g. | *For e.g. | ||
**COMBIN(5.4,2)=10 is equivalent to COMBIN(5,2) | **COMBIN(5.4,2)=10 is equivalent to COMBIN(5,2) | ||
Revision as of 06:12, 18 November 2013
COMBIN(N,R)
- is the number of items.
- is the number of items in each arrangement.
Description
- This function gives the combination of N objects.
- i.e. An arrangement of R objects without any repetition, selected from N different objects is called a combination of N objects taken R at a time.
- Also if the order is not a matter, it is a Combination.
- If order is a matter it is a Permutation.
- A combination is denoted by nCr or .
- A formula for the number of possible combinations of R objects from a set of N objects is where & .
- This function will give Error Result when
- The N&R are non numeric
- The N&R < 0 or N < R
- When we are giving the N&R values in decimals, it will automatically convert in to Integers.
- For e.g.
- COMBIN(5.4,2)=10 is equivalent to COMBIN(5,2)
- COMBIN(5,-2)=NAN, because R is negative.
Examples
| COMBIN(n,r) | n | r | RESULT |
|---|---|---|---|
| COMBIN(12,3) | 12 | 3 | 220 |
| COMBIN(4,4) | 4 | 4 | 1 |
| COMBIN(4,0) | 4 | 0 | 1 |
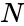 is the number of items.
is the number of items.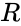 is the number of items in each arrangement.
is the number of items in each arrangement.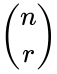 .
.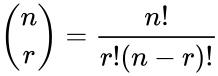 where
where 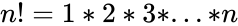 &
&  .
.