Difference between revisions of "Manuals/calci/MULTINOMIAL"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*Multinomial of n set of numbers is defined by:<math> MULTINOMIAL(x1,x2,..xn)=\frac{(x1+x2+…+xn)!}{x1!x2!..xn!}</math> | *Multinomial of n set of numbers is defined by:<math> MULTINOMIAL(x1,x2,..xn)=\frac{(x1+x2+…+xn)!}{x1!x2!..xn!}</math> | ||
This function gives the result as error when | This function gives the result as error when | ||
| − | 1.Any one of the argument is | + | 1.Any one of the argument is non-numeric. |
2.Any one of the argument is <0. | 2.Any one of the argument is <0. | ||
| − | *In <math>MULTINOMIAL(x1,x2...)</math>, <math>x1</math> is required.<math>x2,x3,...</math> | + | *In <math>MULTINOMIAL(x1,x2...)</math>, <math>x1</math> is required.<math>x2,x3,...</math> are optional. |
==Examples== | ==Examples== | ||
Revision as of 03:06, 3 January 2014
MULTINOMIAL(x1,x2,..)
- are numbers
Description
- This function gives the multinomial of the values.
- Multinomial means the ratio of the factorial of a sum of values to the product of factorials.
- Multinomial of n set of numbers is defined by:Failed to parse (syntax error): {\displaystyle MULTINOMIAL(x1,x2,..xn)=\frac{(x1+x2+…+xn)!}{x1!x2!..xn!}}
This function gives the result as error when
1.Any one of the argument is non-numeric. 2.Any one of the argument is <0.
- In , is required. are optional.
Examples
- MULTINOMIAL(10,11)=352716
- MULTINOMIAL(2,3,4,5)=2522520
- MULTINOMIAL(0,1.2,1.3,1.4,1.5)=24
- MULTINOMIAL(0,-1,2)=NAN
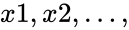 are numbers
are numbers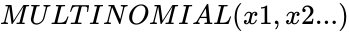 ,
, 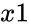 is required.
is required.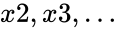 are optional.
are optional.