Difference between revisions of "Manuals/calci/PERMUT"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''PERMUT'''(Number, NumberChosen) where, '''Number''' - represents number of objects. '''NumberChosen'''...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''PERMUT(n,nc)'''</div><br/> |
| + | *<math>n</math> and <math> nc </math> are integers | ||
| − | |||
| − | + | ==Description== | |
| + | *This function gives the number of Permutations for a given number of objects. | ||
| + | *A permutation, also called an arrangement number or order is a rearrangement of the elements of an ordered list. | ||
| + | *A selection of objects in which the order of the objects matters. | ||
| + | *A Permutation is an ordered Combination. | ||
| + | *In <math>PERMUT(n,nc), n</math> is an integer which is indicating the number of objects and nc is an integer which is indicating the number of objects in each permutation. | ||
| + | *For n and nc ,when we are giving in to decimals it will change in to integers. | ||
| + | *The formula for the number of permutation is:<math>n P_k= \frac {n!}{(n-k)!} | ||
| + | *The Permutation is denoted by nPk, Pn,k, or P(n,k).This function will give the result as error when | ||
| + | 1.n and nc are nonnumeric. | ||
| + | 2.Suppose n<=0 or nc<0 or n<nc. | ||
| − | + | ==Examples== | |
| + | #PERMUT(14,2)=182 | ||
| + | #PERMUT(50,5)=254251200 | ||
| + | #PERMUT(10.2,3)=720 | ||
| + | #PERMUT(4,0)=1 | ||
| + | #PERMUT(6,1)=6 | ||
| − | |||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/BINOMDIST | BINOMDIST ]] | |
| − | + | *[[Manuals/calci/COMBIN | COMBIN ]] | |
| + | *[[Manuals/calci/FACT | FACT ]] | ||
| + | *[[Manuals/calci/NEGBINOMDIST | NEGBINOMDIST ]] | ||
| − | + | ==References== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 00:30, 6 January 2014
PERMUT(n,nc)
- and are integers
Description
- This function gives the number of Permutations for a given number of objects.
- A permutation, also called an arrangement number or order is a rearrangement of the elements of an ordered list.
- A selection of objects in which the order of the objects matters.
- A Permutation is an ordered Combination.
- In is an integer which is indicating the number of objects and nc is an integer which is indicating the number of objects in each permutation.
- For n and nc ,when we are giving in to decimals it will change in to integers.
- The formula for the number of permutation is:<math>n P_k= \frac {n!}{(n-k)!}
- The Permutation is denoted by nPk, Pn,k, or P(n,k).This function will give the result as error when
1.n and nc are nonnumeric. 2.Suppose n<=0 or nc<0 or n<nc.
Examples
- PERMUT(14,2)=182
- PERMUT(50,5)=254251200
- PERMUT(10.2,3)=720
- PERMUT(4,0)=1
- PERMUT(6,1)=6
 and
and 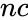 are integers
are integers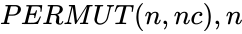 is an integer which is indicating the number of objects and nc is an integer which is indicating the number of objects in each permutation.
is an integer which is indicating the number of objects and nc is an integer which is indicating the number of objects in each permutation.