Difference between revisions of "Manuals/calci/STANDARDIZE"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font face="Arial, sans-serif"><font size="2">'''STANDARDIZE'''</font></font><font face="Arial, sans-serif"><font siz...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''STANDARDIZE(x,m,sd)'''</div><br/> |
| + | *<math>x </math> is the value. | ||
| + | *<math> m </math> is the mean. | ||
| + | *<math> sd </math> is the standard deviation. | ||
| − | |||
| − | < | + | ==Description== |
| + | *This function gives the normalized value of any distribution. | ||
| + | *Standardize is the normalized value for a distribution characterized by a given mean and standard deviation. | ||
| + | *In <math> STANDARDIZE(x,m,sd), x </math> is the value to be normalized , <math> m </math> is the arithmetic mean of the distribution, and <math> sd </math> is the standard deviation of the distribution. | ||
| + | *The equation for the normalized value is:<math> Z= \frac{x-\mu}{\sigma}</math>, where <math> \mu </math> is the arithmetic mean and <math>\sigma </math> is the standard deviation. | ||
| + | *This function will give the result as error when | ||
| + | 1. Any one of the argument is nonnumeric. | ||
| + | 2. sd<=0 | ||
| − | |||
| − | |||
| − | + | ==Examples== | |
| − | + | #=STANDARDIZE(25,20,10.2) = 0.490196078431 | |
| − | + | #=STANDARDIZE(52.5,42,3.25) = 3.230769230769 | |
| − | + | #=STANDARDIZE(30,35,4.21) = -1.187648456057 | |
| − | + | #=STANDARDIZE(2,0,5.3) = 0.377358490566 | |
| + | #=STANDARDIZE(-2,1,6.17) = -0.48622366288 | ||
| − | |||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/NORMDIST | NORMDIST ]] | |
| − | + | *[[Manuals/calci/NORMINV | NORMINV ]] | |
| + | *[[Manuals/calci/NORMSDIST | NORMSDIST ]] | ||
| + | *[[Manuals/calci/NORMSINV | NORMSINV ]] | ||
| − | |||
| − | |||
| − | + | ==References== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 23:41, 2 February 2014
STANDARDIZE(x,m,sd)
- is the value.
- is the mean.
- is the standard deviation.
Description
- This function gives the normalized value of any distribution.
- Standardize is the normalized value for a distribution characterized by a given mean and standard deviation.
- In is the value to be normalized , is the arithmetic mean of the distribution, and is the standard deviation of the distribution.
- The equation for the normalized value is:, where is the arithmetic mean and is the standard deviation.
- This function will give the result as error when
1. Any one of the argument is nonnumeric.
2. sd<=0
Examples
- =STANDARDIZE(25,20,10.2) = 0.490196078431
- =STANDARDIZE(52.5,42,3.25) = 3.230769230769
- =STANDARDIZE(30,35,4.21) = -1.187648456057
- =STANDARDIZE(2,0,5.3) = 0.377358490566
- =STANDARDIZE(-2,1,6.17) = -0.48622366288
See Also
 is the value.
is the value. is the mean.
is the mean.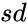 is the standard deviation.
is the standard deviation.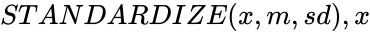 is the value to be normalized ,
is the value to be normalized , 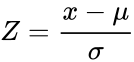 , where
, where 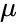 is the arithmetic mean and
is the arithmetic mean and 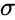 is the standard deviation.
is the standard deviation.