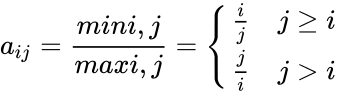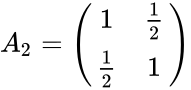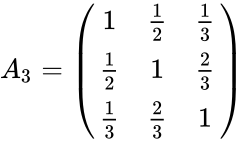Difference between revisions of "Manuals/calci/LEHMER"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
*Also the inverse of a Lehmer matrix is a tridiagonal matrix and is known to be symmetric tridiagonal. | *Also the inverse of a Lehmer matrix is a tridiagonal matrix and is known to be symmetric tridiagonal. | ||
*And the value of this matrix have strictly negative entries (i.e., with positive eigenvalues). | *And the value of this matrix have strictly negative entries (i.e., with positive eigenvalues). | ||
| − | *Example of 2x2 and 3x3 lehmer matrices | + | *Example of 2x2 and 3x3 lehmer matrices are |
<math>A_2=\begin{pmatrix} | <math>A_2=\begin{pmatrix} | ||
1 & \frac{1}{2} \\ | 1 & \frac{1}{2} \\ | ||
Revision as of 09:01, 30 April 2015
MATRIX("LEHMER",order)
- is the order of the Lehmer matrix.
Description
- This function gives the lehmer matrix of order 3.
- The the n×n Lehmer matrix, is the constant symmetric matrix defined by
- Also the inverse of a Lehmer matrix is a tridiagonal matrix and is known to be symmetric tridiagonal.
- And the value of this matrix have strictly negative entries (i.e., with positive eigenvalues).
- Example of 2x2 and 3x3 lehmer matrices are
 is the order of the Lehmer matrix.
is the order of the Lehmer matrix.