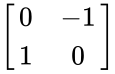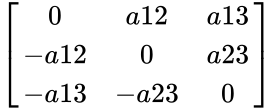Manuals/calci/ANTISYMMETRIC

MATRIX("ANTISYMMETRIC",order)

• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle order } is the order of the Anti diagonal matrix.

Description

• This function gives the matrix of order 3 which is satisfying the anti symmetric properties.
• An antisymmetric matrix is a square matrix that satisfies the identity A=-A^(T) ,where A^(T) is the matrix transpose.
• For example, A= Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} 0 & -1 \\ 1 & 0 \\ \end{bmatrix}}
• So the form of anti symmetric is ${\begin{bmatrix}0&a12&a13\\-a12&0&a23\\-a13&-a23&0\\\end{bmatrix}}$
• Antisymmetric matrices are commonly called "skew symmetric matrices" or "antimetric".
• So in CALCI,users can give the syntax as:
• 1.MATRIX("anti-symmetric")
• 2.MATRIX("antisymmetric")
• 2.MATRIX("skewsymmetric")
• 3.MATRIX("skew-symmetric)
• Here this is case-insensitive.

Examples

• MATRIX("antisymmetric")

0	50	-87
-50	0	12
87	-12	0

• MATRIX("anti-symmetric",4)

0	31	-41	-44
-31	0	67	-88
41	-67	0	100
44	88	-100	0

• MATRIX("skewsymmetric",2)

0	-78
78	0

• MATRIX("skew-symmetric",5)

0	34	-3	79	-7
-34	0	94	81	93
3	-94	0	81	-58
-79	-81	-81	0	-83
7	-93	58	83	0

See Also

• ARROWHEAD
• ANTIDIAGONAL
• MATRIXOPERATORS

References

• Skew Symmetric