Difference between revisions of "Manuals/calci/SCALARPRODUCT"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''DOTPRODUCT(a,b)'''</div><br/> *<math>a</math> and <math>b</math> are any two set values.") |
|||
| Line 1: | Line 1: | ||
| + | <div style="font-size:30px">'''SCALARPRODUCT(a,b)'''</div><br/> | ||
<div style="font-size:30px">'''DOTPRODUCT(a,b)'''</div><br/> | <div style="font-size:30px">'''DOTPRODUCT(a,b)'''</div><br/> | ||
*<math>a</math> and <math>b</math> are any two set values. | *<math>a</math> and <math>b</math> are any two set values. | ||
| + | |||
| + | ==Description== | ||
| + | *This function shows the Scalar product value. | ||
| + | *In <math>DOTPRODUCT(a,b)</math> or <math>SCALARPRODUCT(a,b)</math>,<math>a</math> and <math>b</math> are two set of values with same length. | ||
| + | *Dot product is also called Scalar Product. | ||
| + | *This product is an example of an Inner product. | ||
| + | *Dot product is the algebraic operation which calculates with the two equal length values and gives the single value as result. | ||
| + | *Here a and b are two set of values with any real numbers. | ||
| + | *Also a and b are having same length of values. | ||
| + | *The dot product of two vectors <math>a = [a_1, a_2, ..., a_n]</math>and <math>b = [b_1, b_2, ..., b_n]</math> is defined as: | ||
| + | <math>a.b = \sum_{i=1}^n a_{i}b_{i}= a_1b_1+a_2b_2+...a_nb_n</math> where <math>\Sigma</math> denotes summation notation and <math>n</math> is the dimension of the vector space. | ||
| + | |||
| + | ==Examples== | ||
| + | #SCALARPRODUCT([2,3,4],[9,8,7]) = 70 | ||
| + | #SCALARPRODUCT([3.2,4.5,10.3],[4,8,4.3]) = 93.09 | ||
| + | #SCALARPRODUCT([-6,-15,21],[32.3,19.3,20.3]) = -56.99999999999994 | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/CROSSPRODUCT | CROSSPRODUCT ]] | ||
| + | *[[Manuals/calci/CARTESIANPRODUCT | CARTESIANPRODUCT ]] | ||
| + | *[[Manuals/calci/SCALARPRODUCT | SCALARPRODUCT ]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://tutorial.math.lamar.edu/Classes/CalcII/DotProduct.aspx | Dot Product] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Revision as of 12:49, 5 May 2017
SCALARPRODUCT(a,b)
DOTPRODUCT(a,b)
- and are any two set values.
Description
- This function shows the Scalar product value.
- In or , and are two set of values with same length.
- Dot product is also called Scalar Product.
- This product is an example of an Inner product.
- Dot product is the algebraic operation which calculates with the two equal length values and gives the single value as result.
- Here a and b are two set of values with any real numbers.
- Also a and b are having same length of values.
- The dot product of two vectors and is defined as:
where denotes summation notation and is the dimension of the vector space.
Examples
- SCALARPRODUCT([2,3,4],[9,8,7]) = 70
- SCALARPRODUCT([3.2,4.5,10.3],[4,8,4.3]) = 93.09
- SCALARPRODUCT([-6,-15,21],[32.3,19.3,20.3]) = -56.99999999999994
 and
and 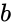 are any two set values.
are any two set values. or
or 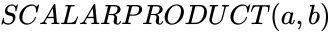 ,
,![{\displaystyle a=[a_{1},a_{2},...,a_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/png/803e8377a0347f4bdd765afc67d41ba8c37d2b8c) and
and ![{\displaystyle b=[b_{1},b_{2},...,b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/png/6b883f746782dc2b06344d9298c02dc25bb0cc07) is defined as:
is defined as: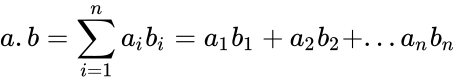 where
where 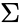 denotes summation notation and
denotes summation notation and  is the dimension of the vector space.
is the dimension of the vector space.