Difference between revisions of "Manuals/calci/EIGENVALUES"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*In linear algebra,an eigen vector or characteristic vector of a linear transformation is a non-zero vector whose direction does not change when that linear transformation is applied to it. | *In linear algebra,an eigen vector or characteristic vector of a linear transformation is a non-zero vector whose direction does not change when that linear transformation is applied to it. | ||
*Let A be a linear transformation represented by a matrix A. | *Let A be a linear transformation represented by a matrix A. | ||
| − | *Let A is an nxn matrix,v is a non zero nx1 vector and <math>\ | + | *Let A is an nxn matrix,v is a non zero nx1 vector and <math>\lambda</math> is a scalar which may be either real or complex. |
*Any value of <math>\Lamda</math> for which this equation has a solution is known as an eigenvalue of the matrix A. | *Any value of <math>\Lamda</math> for which this equation has a solution is known as an eigenvalue of the matrix A. | ||
*It is sometimes also called the characteristic value. | *It is sometimes also called the characteristic value. | ||
Revision as of 15:38, 11 July 2017
EIGENVALUES (Matrix)
- is the array of numeric elements.
Description
- This function shows the Eigen value of the given matrix.
- In , is any matrix values.
- In linear algebra,an eigen vector or characteristic vector of a linear transformation is a non-zero vector whose direction does not change when that linear transformation is applied to it.
- Let A be a linear transformation represented by a matrix A.
- Let A is an nxn matrix,v is a non zero nx1 vector and is a scalar which may be either real or complex.
- Any value of Failed to parse (unknown function "\Lamda"): {\displaystyle \Lamda} for which this equation has a solution is known as an eigenvalue of the matrix A.
- It is sometimes also called the characteristic value.
- The vector, v, which corresponds to this value is called an eigenvector.
- The eigenvalue problem can be rewritten as Failed to parse (unknown function "\Lamda"): {\displaystyle (A-\Lamda.I).v=0} .
- If v is non-zero, this equation will only have a solution if Failed to parse (unknown function "\Lamda"): {\displaystyle |A-\Lamda·I|=0} .
- This equation is called the characteristic equation of A, and is an nth order polynomial in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lamda} with n roots.
- These roots are called the eigenvalues of A.
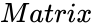 is the array of numeric elements.
is the array of numeric elements.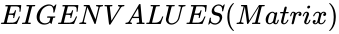 ,
,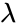 is a scalar which may be either real or complex.
is a scalar which may be either real or complex.