Difference between revisions of "Manuals/calci/SINCP"
Jump to navigation
Jump to search
| Line 3: | Line 3: | ||
==Description== | ==Description== | ||
| − | *This function shows the value of the cardinal sin function. | + | *This function shows the value of the cardinal normalized sin function. |
*In <math>SINCP(X)</math>, <math>X</math> is any real number. | *In <math>SINCP(X)</math>, <math>X</math> is any real number. | ||
| − | *The full name of the function is sine cardinal,but it is commonly referred to by its abbreviation, | + | *The full name of the function is normalized sine cardinal,but it is commonly referred to by its abbreviation, Sincp. |
*The unnormalized SINC function is defined by : | *The unnormalized SINC function is defined by : | ||
<math>SINC(X)=\begin{cases} | <math>SINC(X)=\begin{cases} | ||
| Line 14: | Line 14: | ||
*The value at x = 0 is defined to be the limiting value Sinc(0) = 1. | *The value at x = 0 is defined to be the limiting value Sinc(0) = 1. | ||
*The only difference between the two definitions is in the scaling of the independent variable (the x-axis) by a factor of π. | *The only difference between the two definitions is in the scaling of the independent variable (the x-axis) by a factor of π. | ||
| + | |||
| + | ==Examples== | ||
| + | # SINCP(23) = 8.814971340095828e-17 | ||
| + | # SINCP(-12) = -3.8981718325193755e-17 | ||
| + | # SINCP(45.3) = -0.0056847264326763776 | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/SINC| SINC]] | ||
| + | *[[Manuals/calci/SIN| SIN]] | ||
| + | *[[Manuals/calci/SINH| SINH]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Sinc_function SinC] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Revision as of 12:45, 16 May 2018
SINCP(X)
- is any real number.
Description
- This function shows the value of the cardinal normalized sin function.
- In , is any real number.
- The full name of the function is normalized sine cardinal,but it is commonly referred to by its abbreviation, Sincp.
- The unnormalized SINC function is defined by :
- The normalized SINC function is called as SINCP and it is defined by .
- The value at x = 0 is defined to be the limiting value Sinc(0) = 1.
- The only difference between the two definitions is in the scaling of the independent variable (the x-axis) by a factor of π.
Examples
- SINCP(23) = 8.814971340095828e-17
- SINCP(-12) = -3.8981718325193755e-17
- SINCP(45.3) = -0.0056847264326763776
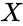 is any real number.
is any real number.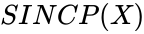 ,
, 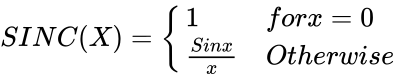
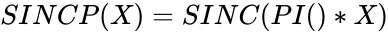 .
.