Difference between revisions of "Manuals/calci/STANDARDIZE"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''STANDARDIZE( | + | <div style="font-size:30px">'''STANDARDIZE (X,Mean,StandardDeviation)'''</div><br/> |
| − | *<math> | + | *<math>X </math> is the value. |
| − | *<math> | + | *<math>Mean</math> is the mean. |
| − | *<math> | + | *<math>StandardDeviation </math> is the standard deviation. |
==Description== | ==Description== | ||
*This function gives the normalized value of any distribution. | *This function gives the normalized value of any distribution. | ||
*Standardize is the normalized value for a distribution characterized by a given mean and standard deviation. | *Standardize is the normalized value for a distribution characterized by a given mean and standard deviation. | ||
| − | *In <math> STANDARDIZE( | + | *In <math> STANDARDIZE (X,Mean,StandardDeviation)</math>, <math>X</math> is the value to be normalized , <math> Mean </math> is the arithmetic mean of the distribution, and <math> StandardDeviation </math> is the standard deviation of the distribution. |
*The equation for the normalized value is: | *The equation for the normalized value is: | ||
<math> Z= \frac{x-\mu}{\sigma}</math>, where <math> \mu </math> is the arithmetic mean and <math>\sigma </math> is the standard deviation. | <math> Z= \frac{x-\mu}{\sigma}</math>, where <math> \mu </math> is the arithmetic mean and <math>\sigma </math> is the standard deviation. | ||
Revision as of 14:38, 12 June 2018
STANDARDIZE (X,Mean,StandardDeviation)
- is the value.
- is the mean.
- is the standard deviation.
Description
- This function gives the normalized value of any distribution.
- Standardize is the normalized value for a distribution characterized by a given mean and standard deviation.
- In , is the value to be normalized , is the arithmetic mean of the distribution, and is the standard deviation of the distribution.
- The equation for the normalized value is:
, where is the arithmetic mean and is the standard deviation.
- This function will give the result as error when
1. Any one of the argument is non-numeric.
2. sd<=0
Examples
- =STANDARDIZE(25,20,10.2) = 0.490196078431
- =STANDARDIZE(52.5,42,3.25) = 3.230769230769
- =STANDARDIZE(30,35,4.21) = -1.187648456057
- =STANDARDIZE(2,0,5.3) = 0.377358490566
- =STANDARDIZE(-2,1,6.17) = -0.48622366288
Related Videos
See Also
References
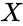 is the value.
is the value.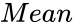 is the mean.
is the mean.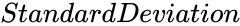 is the standard deviation.
is the standard deviation.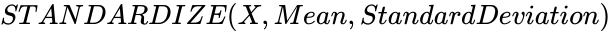 ,
, 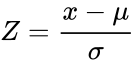 , where
, where 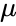 is the arithmetic mean and
is the arithmetic mean and 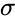 is the standard deviation.
is the standard deviation.