Manuals/calci/EIGENVALUES
Jump to navigation
Jump to search
EIGENVALUES (Matrix)
- is the array of numeric elements.
Description
- This function shows the Eigen value of the given matrix.
- In , is any matrix values.
- In linear algebra,an eigen vector or characteristic vector of a linear transformation is a non-zero vector whose direction does not change when that linear transformation is applied to it.
- Let A be a linear transformation represented by a matrix A.
- Let A is an nxn matrix,v is a non zero nx1 vector and Failed to parse (unknown function "\lamda"): {\displaystyle \lamda} is a scalar which may be either real or complex.
- Any value of Failed to parse (unknown function "\lamda"): {\displaystyle \lamda} for which this equation has a solution is known as an eigenvalue of the matrix A.
- It is sometimes also called the characteristic value.
- The vector, v, which corresponds to this value is called an eigenvector.
- The eigenvalue problem can be rewritten as Failed to parse (unknown function "\lamda"): {\displaystyle (A-\lamda.I).v=0} .
- If v is non-zero, this equation will only have a solution if Failed to parse (unknown function "\lamda"): {\displaystyle |A-\lamda·I|=0} .
- This equation is called the characteristic equation of A, and is an nth order polynomial in Failed to parse (unknown function "\lamda"): {\displaystyle \lamda} with n roots.
- These roots are called the eigenvalues of A.
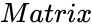 is the array of numeric elements.
is the array of numeric elements.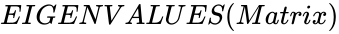 ,
,