Manuals/calci/TTESTTWOSAMPLESUNEQUALVARIANCES
TTESTTWOSAMPLESUNEQUALVARIANCES (Array1,Array2,HypothesizedMeanDifference,Alpha,NewTableFlag)
- and are set of values.
- is the Hypothesized Mean Difference.
- is the significance level.
- is either 0 or 1.
Description
- This function calculating the two Sample for unequal variances determines whether two sample means also distinct.
- We can use this test when both:
- 1.the two sample sizes are may are may not be equal;
- 2. The means and variances are distinct .
- In , and are two arrays of sample values.
- is the Hypothesized Mean Difference. Suppose HypothesizedMeanDifference = 0 which indicates that sample means are hypothesized to be equal.
- is the significance level which ranges from 0 to 1.
- is either 0 or 1.
- "1" is indicating the result will display in new worksheet.Suppose we are omitted the value it will consider the value as "0".
- The t-statistic of this function calculated by:
where
- Here and are unbiased estimators of the variances of two samples. and are the number of data points in two arrays. is not a pooled variance.
- This function will give the result as error when
1. any one of the argument is non-numeric.
2.Alpha>1
Examples
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | 12 | 21 | 9 | 18 | 27 | 37 | 41 |
| 2 | 19 | 8 | 45 | 29 | 14 | 10 | 11 |
- =TTESTTWOSAMPLESUNEQUALVARIANCES(A1:F1,A2:F2,3,0.5,0)
| Variable 1 | Variable 2 | |
|---|---|---|
| Mean | 23.571428571428573 | 19.428571428571427 |
| Variance | 146.61904761904762 | 177.6190476190476 |
| Observations | 7 | 7 |
| Hypothesized Mean Difference | 3 | |
| Degree Of Freedom | 12 | |
| T- Statistics | 0.1679225216302784 | |
| P(T<=t) One-tail | 0.43472054489717515 | |
| T Critical One-Tail | 0 | |
| P(T<=t) Two-tail | 0.8694410897943503 | |
| T Critical Two-Tail | 0.6954828655202375 |
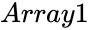 and
and 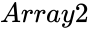 are set of values.
are set of values.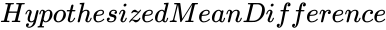 is the Hypothesized Mean Difference.
is the Hypothesized Mean Difference.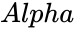 is the significance level.
is the significance level.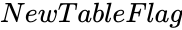 is either 0 or 1.
is either 0 or 1.