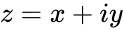Manuals/calci/IMLN

IMLN(Complexnumber)

• $Complexnumber$ is of the form $z=x+iy$

Description

• This function gives the Natural Logarithm of a complex number.
• In $IMLN(Complexnumber)$, where Complexnumber is in the form of $z=x+iy$. i.e $x$ & $y$ are the real numbers.
• And $I$ is the imaginary unit $i={\sqrt {-1}}$.
• Normally Complex logarithm function is an inverse of the Complex exponential function.
• A logarithm of $z$ is a complex number $w$ such that $z=e^{w}$ and it is denoted by $ln(z)$.
• If $z=x+iy$ with $x$ & $y$ are real numbers then natural logarithm of a complex number :

$ln(z)=w=ln(|z|)+iarg(z)=ln({\sqrt {x^{2}+y^{2}}}+itan^{-1}({\frac {y}{x}})$ adding integer multiples of $2\pi i$ gives all the others.

• We can use COMPLEX function to convert real and imaginary number in to a complex number.

ZOS

• The syntax is to calculate the natural logarithm of a complex number in ZOS is $IMLN(Complexnumber)$.
  • $Complexnumber$ is of the form $z=x+iy$
• For e.g.,IMLN("10+17i")

Natural Logarithm of a Complex Number

Examples

1. IMLN("3-2i")=1.28247467873077-0.588002603547568i
2. IMLN("6+7i")=2.22132562824516+0.862170054667226i
3. IMLN("4")=1.38629436111989 +0i
4. IMLN("10i")=2.30258509299405+1.5707963267949i

Related Videos

Log of Complex Number

See Also

• IMLOG10
• IMLOG2
• COMPLEX

References

Imaginary Logarithms