Manuals/calci/TORUS
TORUS (Radius,TubeRadius,w1)
- and are radius value of the circle.
Description
- This function shows the Torus for the given value.
- In , is the radius value of the bigger circle.
- is the radius value of the smaller circle.
- A torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis co planar with the circle. *If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution.
- For example of TORUS are rings, doughnuts, and bagels.
- A torus can be defined parametrically by:
where θ, φ are angles which make a full circle, so that their values start and end at the same point, R is the distance from the center of the tube to the center of the torus, r is the radius of the tube. R is known as the ""major radius"" and r is known as the ""minor radius"".[2] The ratio R divided by r is known as the ""aspect ratio"". The typical doughnut confectionery has an aspect ratio of about 3 to 2"
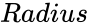 and
and 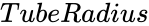 are radius value of the circle.
are radius value of the circle.