Manuals/calci/MINVERSE
Jump to navigation
Jump to search
MINVERSE(arr)
- is the array of numeric elements
Description
- This function gives the inverse matrix for the given matrix.
- We have to find a inverse of a matrix then it should satisfy the following conditions
- 1.A matrix must be a square matrix.
- 2.It's determinant not equal to 0.
- Let <math>A<math> be the 2x2 matrix with the elements A=|a b
c d|.
- Then the inverse of matrix <math>A<math> is denoted by A^-1.So A^-1=|a b|^-=1/ad-bc |d -b
-c a|.
- Now let A be the matrix is of order nXn.
- Then the inverse of A is A^-1= 1/det(A) . adj(A)
- Where adj(A) is the adjoint of A.
- Adjoint is the matrix formed by taking the transpose of the co-factor matrix of a given original matrix.
- Also A.A^-1=A^-1.A=I, where I is the identity matrix.Non-square matrices do not have inverses.
- Not all square matrices have inverses.
- A square matrix which has an inverse is called invertible or non-singular, and a square matrix without an inverse is called non-invertible or singular.
- This function will return the result as error when
1. Any one of the cell is non-numeric or any cell is empty or contain text 2. Suppose number of rows not equal to number of columns
Examples
Matrix A A=(4 3
3 2)
MINVERSE(B5:C6)=(-2 3
3 -4)
MATRIX A A=(3 4
6 8)
MINVERSE(C4:D5)=Null, because its det value is 0. MATRIX A A=(2 3
4 7)
MINVERSE(B4:C5)=(3.5 -1.5
-2 1)
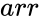 is the array of numeric elements
is the array of numeric elements