Manuals/calci/MATRIXPRODUCT
Jump to navigation
Jump to search
MATRIXPRODUCT (a,b,ConsiderUnits)
- where and are the array of two matrices
Description
- This function gives product of two matrices.
- Matrix multiplication is of two types:
Type 1: A scalar (a constant) is multiplied with the each element of the matrix. Type 2: Multiplication of two matrices.
- We can do the matrix multiplication when the number of columns in the first matrix equals the number of rows in the second matrix.
- For e.g. 4x2 matrix can multiply with 2x3. The matrix product of two arrays and is: where is the row number and is the column number.
- i.e Multiply the elements of each row of 1st matrix by elements of each column of 2nd matrix.
- So the resultant matrix is of the order: Rows of 1st matrix × Columns of 2nd.
- For e.g If we multiply a 4x2 matrix with a 2x3 matrix, the product matrix is of order 4x3.
- Matrix multiplication satisfies the associative and distributive properties.But it is not satisfies the commutative property.
- i.e., Let A,B and C are three matrices, then A(BC)= (AB)C (Associative property)
- A(B+C)= AB+AC and (A+B)C = AC+BC (Distributive properties)
- k(AB)=(kA)B=A(kB)where k is a constant.But (Commutative property)
Examples
1. MATRIXPRODUCT([2,3,4;5,6,7],5)
| 10 | 15 | 20 |
| 25 | 30 | 35 |
2. MATRIXPRODUCT([[6,7,8],[10,12,-22],[7,17,23]],[[20,12,16],[7,8,13],[4,8,9]])
| 120 | 84 | 128 |
| 70 | 96 | -286 |
| 28 | 136 | 207 |
Related Videos
See Also
References
 and
and  are the array of two matrices
are the array of two matrices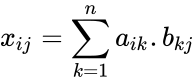 where
where  is the row number and
is the row number and 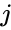 is the column number.
is the column number.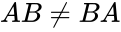 (Commutative property)
(Commutative property)