Manuals/calci/NQUEENS
From ZCubes Wiki
Jump to navigation
Jump to search
NQUEENS (GridSize)
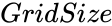 is any positive integer.
is any positive integer.
Description
- This functions creates the N-queens puzzle.
- In
 ,
, 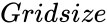 is the size of the row and columns.
is the size of the row and columns.
- Generally eight queens puzzle is the problem of placing eight chess queens on an 8x8 chessboard so that no two queens attack each other.
- Thus, a solution requires that no two queens share the same row, column or diagonal.
- The eight queens puzzle is a great example of the more general N Queens problem of placing N non attacking queens on an nxn chessboard where solutions exist for all natural numbers n with the exception of n=2 and n=3.
- This function will return the result as "0" when the value of the Grid size is 2 or 3.
- Also this will return as Error when the parameter value is non positive integer.
Examples
1. NQUEENS(4)
1
| _|Q|_|_|
|
| _|_|_|Q|
|
| Q|_|_|_|
|
| _|_|Q|_|
|
2
| _|Q|_|_|
|
| _|_|_|Q|
|
| Q|_|_|_|
|
| _|_|Q|_|
|
2 Solutions
1
| _|Q|_|_|_|_|
|
| _|_|_|Q|_|_|
|
| _|_|_|_|_|Q|
|
| Q|_|_|_|_|_|
|
| _|_|Q|_|_|_|
|
| _|_|_|_|Q|_|
|
2
| _|_|Q|_|_|_|
|
| _|_|_|_|_|Q|
|
| _|Q|_|_|_|_|
|
| _|_|_|_|Q|_|
|
| Q|_|_|_|_|_|
|
| _|_|_|Q|_|_|
|
3
| _|_|_|Q|_|_|
|
| Q|_|_|_|_|_|
|
| _|_|_|_|Q|_|
|
| _|Q|_|_|_|_|
|
| _|_|_|_|_|Q|
|
| _|_|Q|_|_|_|
|
4
| _|_|_|_|Q|_|
|
| _|_|Q|_|_|_|
|
| Q|_|_|_|_|_|
|
| _|_|_|_|_|Q|
|
| _|_|_|Q|_|_|
|
| _|Q|_|_|_|_|
|
4 Solutions
Related Videos
See Also
References
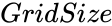 is any positive integer.
is any positive integer. ,
, 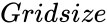 is the size of the row and columns.
is the size of the row and columns.