Difference between revisions of "Manuals/calci/BETADIST"
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font size="3"><font face="Times New Roman">'''BETADIST''' ('''N''',''' alpha, beta, X, Y''')</font></font> <font ...") |
|||
| (43 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''BETADIST (Number,Alpha,Beta,LowerBound,UpperBound)'''</div><br/> |
| + | *<math>Number</math> is the value between <math>LowerBound</math> and <math>UpperBound</math> | ||
| + | *<math>Alpha</math> and <math>Beta</math> are the value of the shape parameter | ||
| + | *<math>LowerBound</math> & <math>UpperBound</math> the lower and upper limit to the interval of <math>Number</math>. | ||
| + | **BETADIST(),returns the Beta Cumulative Distribution Function. | ||
| − | < | + | ==Description== |
| + | *This function gives the Cumulative Beta Probability Density function. | ||
| + | *The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by <math>\alpha</math> and <math>\beta</math>. | ||
| + | *The Beta Distribution is also known as the Beta Distribution of the first kind. | ||
| + | *In <math>(Number,Alpha,Beta,LowerBound,UpperBound)</math>, <math>Number</math> is the value between <math>LowerBound</math> and <math>UpperBound</math>. | ||
| + | *Alpha is the value of the shape parameter. | ||
| + | *Beta is the value of the shape parameter | ||
| + | *<math>LowerBound</math> and <math>UpperBound</math>(optional) are the Lower and Upper limit to the interval of <math>Number</math>. | ||
| + | *Normally <math>Number</math> lies between the limit <math>LowerBound</math> and <math>UpperBound</math>, suppose when we are omitting <math>LowerBound</math> and <math>UpperBound</math> value, by default <math>Number</math> value with in 0 and 1. | ||
| + | *The Probability Density Function of the beta distribution is: | ||
| + | <math>f(x)=\frac{x^{\alpha-1}(1-x)^{ \beta-1}}{B(\alpha,\beta)},</math> where <math>0 \le x \le 1</math>; <math>\alpha,\beta >0 </math> and <math>B(\alpha,\beta)</math> is the Beta function. | ||
| + | *The formula for the Cumulative Beta Distribution is called the Incomplete Beta function ratio and it is denoted by <math>I_x</math> and is defined as : | ||
| + | <math>F(x)=I_x(\alpha,\beta)</math>=<math>\int_{0}^{x}f(x)=\frac{t^{\alpha-1}(1-t)^{ \beta-1}dt}{B(\alpha,\beta)}</math>, where <math>0 \le t \le 1</math> ; <math>\alpha,\beta>0</math> and <math>B(\alpha,\beta)</math> is the Beta function. | ||
| + | *This function will give the result as error when | ||
| + | 1.Any one of the arguments are non-numeric. | ||
| + | 2.<math>Alpha \le 0</math> or <math>Beta \le 0</math> | ||
| + | 3.<math>Number<LowerBound</math> ,<math>Number>UpperBound</math>, or <math>LowerBound=UpperBound</math> | ||
| + | *we are not mentioning the limit values <math>LowerBound</math> and <math>UpperBound</math>, | ||
| + | *By default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1. | ||
| − | + | ==ZOS== | |
| − | < | + | *The syntax is to calculate BEATDIST in ZOS is <math>BETADIST (Number,Alpha,Beta,LowerBound,UpperBound)</math>. |
| + | **<math>Number</math> is the value between LowerBound and UpperBound | ||
| + | **<math>alpha</math> and <math>beta</math> are the value of the shape parameter. | ||
| + | *For e.g.,BETADIST(11..13,3,5,8,14) | ||
| + | *BETADIST(33..35,5..6,10..11,30,40) | ||
| − | |||
| − | + | ==Examples== | |
| + | #=BETADIST(0.4,8,10) = 0.35949234293309396 | ||
| + | #=BETADIST(3,5,9,2,6) = 0.20603810250759128 | ||
| + | #=BETADIST(9,4,2,8,11) = 0.04526748971193415 | ||
| + | #=BETADIST(5,-1,-2,4,7) = #N/A (ALPHA GREATER THAN (OR) NOT EQUAL TO 0) | ||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|aZjUTx-E0Pk|280|center|Beta Distribution}} | |
| − | - | ||
| − | |||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/BETAINV | BETAINV]] | ||
| + | *[[Manuals/calci/ALL | All Functions]] | ||
| − | + | ==References== | |
| − | + | [http://en.wikipedia.org/wiki/Beta_distribution Beta Distribution] | |
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 03:57, 2 June 2020
- is the value between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LowerBound} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UpperBound}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Alpha} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Beta} are the value of the shape parameter
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LowerBound}
& Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UpperBound}
the lower and upper limit to the interval of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number}
.
- BETADIST(),returns the Beta Cumulative Distribution Function.
Description
- This function gives the Cumulative Beta Probability Density function.
- The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} .
- The Beta Distribution is also known as the Beta Distribution of the first kind.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (Number,Alpha,Beta,LowerBound,UpperBound)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} is the value between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LowerBound} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UpperBound} .
- Alpha is the value of the shape parameter.
- Beta is the value of the shape parameter
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LowerBound} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UpperBound} (optional) are the Lower and Upper limit to the interval of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} .
- Normally Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} lies between the limit Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LowerBound} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UpperBound} , suppose when we are omitting Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LowerBound} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UpperBound} value, by default Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} value with in 0 and 1.
- The Probability Density Function of the beta distribution is:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=\frac{x^{\alpha-1}(1-x)^{ \beta-1}}{B(\alpha,\beta)},} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \le x \le 1} ; Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha,\beta >0 } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(\alpha,\beta)} is the Beta function.
- The formula for the Cumulative Beta Distribution is called the Incomplete Beta function ratio and it is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_x} and is defined as :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x)=I_x(\alpha,\beta)} =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{x}f(x)=\frac{t^{\alpha-1}(1-t)^{ \beta-1}dt}{B(\alpha,\beta)}} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \le t \le 1} ; Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha,\beta>0} and is the Beta function.
- This function will give the result as error when
1.Any one of the arguments are non-numeric.
2.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Alpha \le 0}
or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Beta \le 0}
3.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number<LowerBound}
,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number>UpperBound}
, or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LowerBound=UpperBound}
- we are not mentioning the limit values Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LowerBound} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UpperBound} ,
- By default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1.
ZOS
- The syntax is to calculate BEATDIST in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BETADIST (Number,Alpha,Beta,LowerBound,UpperBound)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} is the value between LowerBound and UpperBound
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle alpha} and are the value of the shape parameter.
- For e.g.,BETADIST(11..13,3,5,8,14)
- BETADIST(33..35,5..6,10..11,30,40)
Examples
- =BETADIST(0.4,8,10) = 0.35949234293309396
- =BETADIST(3,5,9,2,6) = 0.20603810250759128
- =BETADIST(9,4,2,8,11) = 0.04526748971193415
- =BETADIST(5,-1,-2,4,7) = #N/A (ALPHA GREATER THAN (OR) NOT EQUAL TO 0)
Related Videos
See Also
References
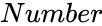 is the value between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LowerBound}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UpperBound}
is the value between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LowerBound}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UpperBound}
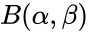 is the Beta function.
is the Beta function.
 are the value of the shape parameter.
are the value of the shape parameter.