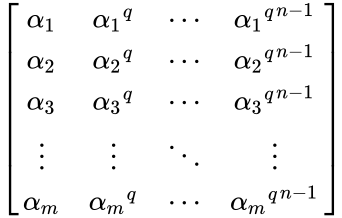Difference between revisions of "Manuals/calci/MOORE"
Jump to navigation
Jump to search
| (6 intermediate revisions by 2 users not shown) | |||
| Line 8: | Line 8: | ||
*But it is unrelated to the Moore determinant of a quaternionic Hermitian matrix. | *But it is unrelated to the Moore determinant of a quaternionic Hermitian matrix. | ||
*The Moore matrix has successive powers of the applied to the first column, so it is an mxn matrix of the form: | *The Moore matrix has successive powers of the applied to the first column, so it is an mxn matrix of the form: | ||
| − | <math>\begin{bmatrix} | + | <math> |
| − | \alpha_1 & \alpha_1^ | + | \begin{bmatrix} |
| − | \alpha_2 & \alpha_2^ | + | \alpha_1 & {\alpha_1}^q & \cdots & {{\alpha_1}^q}^{n-1} \\ |
| − | \alpha_3 & \alpha_3^ | + | \alpha_2 & {\alpha_2}^q & \cdots & {{\alpha_2}^q}^{n-1} \\ |
| − | \vdots & \ddots & \vdots \\ | + | \alpha_3 & {\alpha_3}^q & \cdots & {{\alpha_3}^q}^{n-1} \\ |
| − | \alpha_m & \alpha_m^ | + | \vdots & \vdots & \ddots & \vdots\\ |
| − | \end{bmatrix} </math> | + | \alpha_m & {\alpha_m}^q & \cdots & {{\alpha_m}^q}^{n-1} \\ |
| + | \end{bmatrix} | ||
| + | </math> | ||
*In calci, MATRIX("moore") is giving the matrixwith the element 1 of order 3. | *In calci, MATRIX("moore") is giving the matrixwith the element 1 of order 3. | ||
*And MATRIX("moore",4,1..4) is giving Moore matrix starting element 1 to 4 of order 4. | *And MATRIX("moore",4,1..4) is giving Moore matrix starting element 1 to 4 of order 4. | ||
| + | |||
| + | ==Examples== | ||
| + | *1.MATRIX("moore") = 1 | ||
| + | *2.MATRIX("moore",3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 || 1 || 1 | ||
| + | |} | ||
| + | *3.MATRIX("moore",5,1..5) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 || 1 || 1 | ||
| + | |- | ||
| + | | 2 || 4 || 16 || 256 || 65536 | ||
| + | |- | ||
| + | | 3 || 9 || 81 || 6561 || 43046721 | ||
| + | |- | ||
| + | | 4 || 16 || 256 || 65536 || 4294967296 | ||
| + | |- | ||
| + | | 5 || 25 || 625 || 390625 || 152587890625 | ||
| + | |} | ||
| + | *4.MATRIX("moore",4,3..7,"",2.3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 3 || 12.513502532843182 || 334.1730615222005 || 638460.9005874459 | ||
| + | |- | ||
| + | | 4 || 24.251465064166364 || 1530.7256306021752 || 21147737.669320222 | ||
| + | |- | ||
| + | | 5 || 40.51641491731905 || 4983.693475030862 || 319424366.94628483 | ||
| + | |- | ||
| + | | 6 || 61.623714938749366 || 13074.350231574774 || 2936069039.087338 | ||
| + | |} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | *[[Manuals/calci/HANKEL| HANKEL]] | ||
| + | *[[Manuals/calci/HERMITIAN| HERMITIAN]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Moore_matrix Moore matrix] | ||
Latest revision as of 01:30, 26 October 2015
MATRIX("MOORE",order)
- is the size of the Moore matrix.
Description
- This function gives the moore matrix of order 3 with the element 1.
- A moore matrix, is a square matrix over a finite field.
- When moore matrix is a square matrix, then its deteminant is called a Moore determinant.
- But it is unrelated to the Moore determinant of a quaternionic Hermitian matrix.
- The Moore matrix has successive powers of the applied to the first column, so it is an mxn matrix of the form:
- In calci, MATRIX("moore") is giving the matrixwith the element 1 of order 3.
- And MATRIX("moore",4,1..4) is giving Moore matrix starting element 1 to 4 of order 4.
Examples
- 1.MATRIX("moore") = 1
- 2.MATRIX("moore",3)
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| 1 | 1 | 1 |
- 3.MATRIX("moore",5,1..5)
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 16 | 256 | 65536 |
| 3 | 9 | 81 | 6561 | 43046721 |
| 4 | 16 | 256 | 65536 | 4294967296 |
| 5 | 25 | 625 | 390625 | 152587890625 |
- 4.MATRIX("moore",4,3..7,"",2.3)
| 3 | 12.513502532843182 | 334.1730615222005 | 638460.9005874459 |
| 4 | 24.251465064166364 | 1530.7256306021752 | 21147737.669320222 |
| 5 | 40.51641491731905 | 4983.693475030862 | 319424366.94628483 |
| 6 | 61.623714938749366 | 13074.350231574774 | 2936069039.087338 |
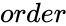 is the size of the Moore matrix.
is the size of the Moore matrix.