Difference between revisions of "Manuals/calci/ADJ"
Jump to navigation
Jump to search
| (3 intermediate revisions by the same user not shown) | |||
| Line 60: | Line 60: | ||
1.adj([[10,12],[-14,21]]) | 1.adj([[10,12],[-14,21]]) | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | |||
|- | |- | ||
| 21 ||-12 | | 21 ||-12 | ||
| Line 68: | Line 67: | ||
2.adj([[4,5,8],[3,-6,-9],[10,-12,4]]) | 2.adj([[4,5,8],[3,-6,-9],[10,-12,4]]) | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | |||
|- | |- | ||
| -132 ||-116||2.9999999999999982 | | -132 ||-116||2.9999999999999982 | ||
| Line 79: | Line 77: | ||
3.adj([[5,-2,2,7],[1,0,0,3], [-3,1,5,0], [3,-1,-9,4]]) | 3.adj([[5,-2,2,7],[1,0,0,3], [-3,1,5,0], [3,-1,-9,4]]) | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | |||
|- | |- | ||
| -12 ||76||-60 ||-36 | | -12 ||76||-60 ||-36 | ||
| Line 89: | Line 86: | ||
| 4 ||3.9999999999999982 || 20 || 12 || | | 4 ||3.9999999999999982 || 20 || 12 || | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=oHzpMgKuI9Q|280|center|Adjoint Matrix}} | ||
==See Also== | ==See Also== | ||
| Line 97: | Line 98: | ||
==References== | ==References== | ||
*[https://en.wikipedia.org/wiki/Adjugate_matrix Adjugate matrix] | *[https://en.wikipedia.org/wiki/Adjugate_matrix Adjugate matrix] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 13:24, 9 April 2019
ADJ(Array)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array} is the set of values.
Description
- This function shows the Adjoint of a given matrix.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ADJ(Array)} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array} is the set of matrix values.
- Adjoint of a matrix is called adjugate, classical adjoint, or adjunct.Adjoint of a matrix formed by taking the transpose of the cofactor matrix of a given original Square matrix.
- Adjoint of matrix A is written by .
- The adjugate of A is the transpose of the cofactor matrix C of A, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle adj(A)= C^T} .
- Also adjoint of a matrix is defined by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle adj(A)= det(A).A^{-1}} .
- The adjugate of 1x1 matrix is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I=(1)} .
- The adjugate of 2x2 matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle :A= \begin{pmatrix} a & b \\ c & d \end{pmatrix} } is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle adj(A)=\begin{pmatrix} d & -b \\ -c & a \end{pmatrix}} .
- Consider3x3 matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} } .
- Its adjugate is the transpose of its cofactor matrix:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle adj(A)=C^{T} = \begin{pmatrix} +\begin{vmatrix} a_ {22}& a_{23} \\ a_ {32}& a_{33} \end{vmatrix} & - \begin{vmatrix} a_ {12}& a_{13} \\ a_ {32}& a_{33} \end{vmatrix} & +\begin{vmatrix} a_ {12}& a_{13} \\ a_ {22}& a_{23} \end{vmatrix} \\ +\begin{vmatrix} a_ {21}& a_{23} \\ a_ {31}& a_{33} \end{vmatrix} & - \begin{vmatrix} a_ {11}& a_{13} \\ a_ {31}& a_{33} \end{vmatrix} & +\begin{vmatrix} a_ {11}& a_{13} \\ a_ {21}& a_{23} \end{vmatrix} \\ +\begin{vmatrix} a_ {21}& a_{22} \\ a_ {31}& a_{32} \end{vmatrix} & - \begin{vmatrix} a_ {11}& a_{12} \\ a_ {31}& a_{32} \end{vmatrix} & +\begin{vmatrix} a_ {11}& a_{12} \\ a_ {21}& a_{22} \end{vmatrix} \\ \end{pmatrix}}
Examples
1.adj([[10,12],[-14,21]])
| 21 | -12 |
| 14 | 10 |
2.adj([[4,5,8],[3,-6,-9],[10,-12,4]])
| -132 | -116 | 2.9999999999999982 |
| -102 | -64 | 60 |
| 24 | 98 | -39 |
3.adj([[5,-2,2,7],[1,0,0,3], [-3,1,5,0], [3,-1,-9,4]])
| -12 | 76 | -60 | -36 | |
| -56 | 207.99999999999997 | -81.99999999999999 | -57.99999999999999 | |
| 4 | 3.999999999999999 | -1.9999999999999998 | -10 | |
| 4 | 3.9999999999999982 | 20 | 12 |
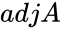 .
.