Difference between revisions of "Manuals/calci/MATRIXADJOINT"
Jump to navigation
Jump to search
| (One intermediate revision by the same user not shown) | |||
| Line 60: | Line 60: | ||
==Examples== | ==Examples== | ||
1. MATRIXADJOINT([4]) = 1 | 1. MATRIXADJOINT([4]) = 1 | ||
| − | 2. MATRIXADJOINT([2,3;7,8]) | + | |
| + | 2.MATRIXADJOINT([2,3;7,8]) | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 76: | Line 77: | ||
| 24.999999999999996|| 114 || -24 | | 24.999999999999996|| 114 || -24 | ||
|} | |} | ||
| + | |||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=oHzpMgKuI9Q&t=7s|280|center|Matrix Adjoint}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 13:26, 12 April 2019
MATRIXADJOINT (a)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is any set of values.
Description
- This function shows the Adjoint of a given matrix.
- In ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is the set of matrix values.
- Adjoint of a matrix is called adjugate, classical adjoint, or adjunct.
- Adjoint of a matrix formed by taking the transpose of the cofactor matrix of a given original Square matrix.
- Adjoint of matrix A is written by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle adj A} .
- The adjugate of A is the transpose of the cofactor matrix C of A, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle adj(A)= C^T} .
- Also adjoint of a matrix is defined by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle adj(A)= det(A).A^{-1}} .
- The adjugate of 1x1 matrix is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I=(1)} .
- The adjugate of 2x2 matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle :A= \begin{pmatrix} a & b \\ c & d \end{pmatrix} } is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle adj(A)=\begin{pmatrix} d & -b \\ -c & a \end{pmatrix}} .
- Consider3x3 matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} } .
- Its adjugate is the transpose of its cofactor matrix:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle adj(A)=C^{T} = \begin{pmatrix} +\begin{vmatrix} a_ {22}& a_{23} \\ a_ {32}& a_{33} \end{vmatrix} & - \begin{vmatrix} a_ {12}& a_{13} \\ a_ {32}& a_{33} \end{vmatrix} & +\begin{vmatrix} a_ {12}& a_{13} \\ a_ {22}& a_{23} \end{vmatrix} \\ +\begin{vmatrix} a_ {21}& a_{23} \\ a_ {31}& a_{33} \end{vmatrix} & - \begin{vmatrix} a_ {11}& a_{13} \\ a_ {31}& a_{33} \end{vmatrix} & +\begin{vmatrix} a_ {11}& a_{13} \\ a_ {21}& a_{23} \end{vmatrix} \\ +\begin{vmatrix} a_ {21}& a_{22} \\ a_ {31}& a_{32} \end{vmatrix} & - \begin{vmatrix} a_ {11}& a_{12} \\ a_ {31}& a_{32} \end{vmatrix} & +\begin{vmatrix} a_ {11}& a_{12} \\ a_ {21}& a_{22} \end{vmatrix} \\ \end{pmatrix}}
Examples
1. MATRIXADJOINT([4]) = 1
2.MATRIXADJOINT([2,3;7,8])
| 8 | -3 |
| -7 | 2 |
3.MATRIXADJOINT([-6,12,5;3,-2,9;8,3,3])
| -33 | -21 | 118 |
| 63 | -58 | 69 |
| 24.999999999999996 | 114 | -24 |
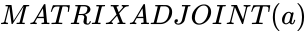 ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a}
is the set of matrix values.
,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a}
is the set of matrix values.