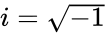Difference between revisions of "Manuals/calci/MAKECOMPLEXIPLUS"
Jump to navigation
Jump to search
| (One intermediate revision by the same user not shown) | |||
| Line 14: | Line 14: | ||
*To mention <math>i</math> and <math>j</math>, we must use the lower case only | *To mention <math>i</math> and <math>j</math>, we must use the lower case only | ||
*In a complex number <math>z</math> real part is denoted by <math>Re(z)</math> & imaginary part is denoted by <math>Im(z)</math>. | *In a complex number <math>z</math> real part is denoted by <math>Re(z)</math> & imaginary part is denoted by <math>Im(z)</math>. | ||
| − | *MAKECOMPLEXIPLUS returns the error value, when <math> | + | *MAKECOMPLEXIPLUS returns the error value, when <math>Real</math> and <math>Imaginary</math> are non-numeric. |
| − | |||
*A Complex number whose real part is zero is said to be purely imaginary. | *A Complex number whose real part is zero is said to be purely imaginary. | ||
*A Complex number whose imaginary part is zero is a real number. In that cases we have to assign '0' for that part. | *A Complex number whose imaginary part is zero is a real number. In that cases we have to assign '0' for that part. | ||
| Line 33: | Line 32: | ||
#=MAKECOMPLEXIPLUS(1,-10,"j") = 1-j10 | #=MAKECOMPLEXIPLUS(1,-10,"j") = 1-j10 | ||
#=MAKECOMPLEXIPLUS(1,0) = 1+i0 | #=MAKECOMPLEXIPLUS(1,0) = 1+i0 | ||
| − | #=MAKECOMPLEXIPLUS(1..3,-5) = 1- | + | #=MAKECOMPLEXIPLUS(1..3,-5) |
| + | {| class="wikitable" | ||
| + | |- class="even" | ||
| + | !Real | ||
| + | !Imaginary | ||
| + | !MAKECOMPLEXIPLUS | ||
| + | |- class="odd" | ||
| + | |1 | ||
| + | | -5 | ||
| + | |1-5ⅈ | ||
| + | |- class="even" | ||
| + | |2 | ||
| + | | -5 | ||
| + | |2-5ⅈ | ||
| + | |- class="odd" | ||
| + | |3 | ||
| + | | -5 | ||
| + | |3-5ⅈ | ||
| + | |} | ||
==Related Videos== | ==Related Videos== | ||
Latest revision as of 06:48, 29 September 2021
MAKECOMPLEXIPLUS (Real,Imaginary)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Real} is the real part of the complex number.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Imaginary} is the imaginary part of the complex number.
Description
- MAKECOMPLEXIPLUS function converts the imaginary coefficient of a complex number into 'positive' coefficient.
- A complex number is a combination of a real and an imaginary number.
- A number which is positive or negative, rational or irrational or decimals are called real numbers.
- An Imaginary number is a number that when squring it gives a negative result.
- For e.g. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {-4}^2 =16} . Because a negative times a negative is positive.
- A complex number is a number is in the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = a + bi} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} are real numbers and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} is the imaginary unit. Where
- To mention Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} , we must use the lower case only
- In a complex number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} real part is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Re(z)} & imaginary part is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Im(z)} .
- MAKECOMPLEXIPLUS returns the error value, when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Real} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Imaginary} are non-numeric.
- A Complex number whose real part is zero is said to be purely imaginary.
- A Complex number whose imaginary part is zero is a real number. In that cases we have to assign '0' for that part.
- =MAKECOMPLEXIPLUS (5,2) gives Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5+i2}
- =MAKECOMPLEXIPLUS (5,2,["j"]) gives Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5+j2}
ZOS
- The syntax is to calculate MAKECOMPLEXIPLUS in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MAKECOMPLEXIPLUS (Real,Imaginary)}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle REAL} is the real part.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMAGINARY} is the imaginary part.
Examples
- =MAKECOMPLEXIPLUS(4,-5) = 4-i5
- =MAKECOMPLEXIPLUS(4,5) = 4+i5
- =MAKECOMPLEXIPLUS(1,-10,"j") = 1-j10
- =MAKECOMPLEXIPLUS(1,0) = 1+i0
- =MAKECOMPLEXIPLUS(1..3,-5)
| Real | Imaginary | MAKECOMPLEXIPLUS |
|---|---|---|
| 1 | -5 | 1-5ⅈ |
| 2 | -5 | 2-5ⅈ |
| 3 | -5 | 3-5ⅈ |
Related Videos
See Also
References