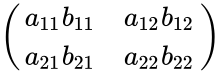Difference between revisions of "Manuals/calci/HADAMARDPRODUCT"
Jump to navigation
Jump to search
| Line 43: | Line 43: | ||
==Related Videos== | ==Related Videos== | ||
| − | {{#ev:youtube|v=hbU5V-ccA9I|280|center| | + | {{#ev:youtube|v=hbU5V-ccA9I|280|center|Hadamard Product}} |
==See Also== | ==See Also== | ||
Latest revision as of 12:48, 9 April 2019
HADAMARDPRODUCT (a,b)
- and are any two matrices.
Description
- This function shows the value of the Hadamard product.
- In , and are two matrices.
- Hadamard product is also called Schur product or entrywise product.
- The Hadamard product is associative,commutative and distributive.
- This product is the multiplied value of the each corresponding entries with the given two same dimension matrices.
- Hadamard product is defined by,For two matrices, A and B of the same dimension mxn, the Hadamard product , is a matrix, of the same dimension as the operands, with elements given by:
- Hadamard Product of order 2 is calculated by:
=
Examples
1. HADAMARDPRODUCT([[2,3],[10,14]],[[6,4],[8,3]])
| 12 | 12 |
| 80 | 42 |
2. HADAMARDPRODUCT([[6,3,10],[5,-7,12],[4,2,6]],[[4,5,6],[9,2,-5],[12,13,7]])
| 24 | 15 | 60 |
| 45 | -14 | -60 |
| 48 | 26 | 42 |
Related Videos
See Also
References
 and
and 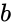 are any two matrices.
are any two matrices.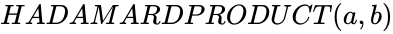 ,
,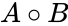 , is a matrix, of the same dimension as the operands, with elements given by:
, is a matrix, of the same dimension as the operands, with elements given by: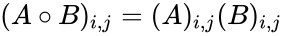
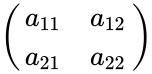

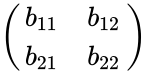 =
=