Difference between revisions of "Manuals/calci/FTEST"

From ZCubes Wiki
Jump to navigation Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''FTEST''' ('''arr1''',''' arr2''') Where '''arr1'''   is the first array or range of data and a'''rr2''' is t...")
 
 
(28 intermediate revisions by 4 users not shown)
Line 1: Line 1:
−
<div id="6SpaceContent" class="zcontent" align="left">
+
<div style="font-size:30px">'''FTEST(Array1,Array2)'''</div><br/>
 +
*<math>Array1</math> and <math>Array2 </math> are array of data.
 +
**FTEST(), returns the result of an F-test.
  
−
'''FTEST''' ('''arr1''',''' arr2''')
+
==Description==
 +
*This function gives the result of F-test.
 +
*The F-test is designed to test if two population variances are equal.
 +
*It does this by comparing the ratio of two variances.
 +
*So, if the variances are equal, the ratio of the variances will be 1.
 +
*Let X1,...Xn and Y1,...Ym be independent samples each have a Normal Distribution .
 +
*It's sample means:
 +
<math>\bar X=\frac{1}{n} \sum_{i=1}^n Xi</math>
 +
and 
 +
:<math>\bar Y =\frac {1}{m} \sum_{i=1}^m Yi</math> .
 +
*The sample variances :
 +
<math>SX^2=\frac{1}{n-1} \sum_{i=1}^n (Xi-\bar X)^2</math>
 +
and
 +
:<math>SY^2=\frac{1}{m-1} \sum_{i=1}^m (Yi-\bar Y)^2</math>
 +
*Then the Test Statistic = <math>\frac {Sx^2}{Sy^2}</math> has an F-distribution with 'n−1' and  'm−1' degrees of freedom.
 +
*In FTEST(Array1,Array2) where <math>Array1</math> is the data of  first array, <math>Array2</math> is the data of second array.
 +
*The array may be any numbers, names, or references that contains numbers.
 +
*values are not considered if the array contains any text, logical values or empty cells.
 +
When the <math>Array1</math> or <math>Array2</math> is less than 2 or the variance of the array value is zero, then this function will return the result as error.
  
−
Where '''arr1'''   is the first array or range of data and a'''rr2''' is the second array or range of data.
+
==ZOS==
 +
*The syntax is to calculate FTEST in ZOS is <math>FTEST(Array1,Array2)</math>.
 +
**<math>Array1</math> and <math>Array2 </math> are array of data.
 +
*For e.g.,FTEST([15,29,30],[62,74,80])
 +
{{#ev:youtube|y_uVl6UbHtE|280|center|F-Test}}
  
−
</div>
+
==Examples==
−
----
+
1.
−
<div id="1SpaceContent" class="zcontent" align="left">
+
{| class="wikitable"  
 +
|+ DATA1
 +
|-
 +
| 15
 +
| 27
 +
| 19
 +
| 32
 +
|}
  
−
F-test calculates the two-tailed probability that the variances in arr1 and arr2 are not significantly different.
+
{| class="wikitable"
 +
|+ DATA2
 +
|-  
 +
| 21
 +
| 12
 +
| 30
 +
| 11
 +
|}
  
−
</div>
+
=FTEST(B4:B8,C4:C8)=0.81524906747183
−
----
 
−
<div id="7SpaceContent" class="zcontent" align="left">
 
  
−
·          The arguments must either be numbers or names, arrays, or references that contain numbers.
+
2.
 +
{| class="wikitable"
 +
|+ DATA1
 +
|-
 +
| 5
 +
| 8
 +
| 12
 +
| 45
 +
| 23
 +
|}
  
−
·          When the number of data points in arr1 or arr2 is less than 2, or if the variance of arr1 or arr2 is zero FTEST displays NaN.
+
{| class="wikitable"
 +
|+ DATA2
 +
|-
 +
| 10
 +
| 20
 +
| 30
 +
| 40
 +
| 50
 +
|}
 +
=FTEST(A1:A5,C1:C5)=0.9583035732212274 
 +
3.
 +
{| class="wikitable"
 +
|+ DATA1
 +
|-
 +
| 14
 +
| 26
 +
| 37
 +
|}
  
−
</div>
+
{| class="wikitable"  
−
----
+
|+ DATA2
−
<div id="12SpaceContent" class="zcontent" align="left"><div class="ZEditBox" align="left">FTEST</div></div>
+
|-  
−
----
+
| 45
−
<div id="10SpaceContent" class="zcontent" align="left"><div class="ZEditBox" align="justify">Syntax </div><div class="ZEditBox"><center></center></div></div>
+
| 82
−
----
+
| 21
−
<div id="4SpaceContent" class="zcontent" align="left"><div class="ZEditBox" align="justify">Remarks </div></div>
+
|17
−
----
+
|}
−
<div id="3SpaceContent" class="zcontent" align="left"><div class="ZEditBox" align="justify">Examples </div></div>
+
FTEST(B1:B3,C1:C4} = 0.26412211240525474
−
----
 
−
<div id="11SpaceContent" class="zcontent" align="left"><div class="ZEditBox" align="justify">Description </div></div>
 
−
----
 
−
<div id="2SpaceContent" class="zcontent" align="left">
 
  
−
{| id="TABLE3" class="SpreadSheet blue"
+
4.
−
|- class="even"
+
{| class="wikitable"  
−
| class="  " |
+
  |+ DATA1
−
<div id="2Space_Copy" title="Click and Drag over to AutoFill other cells."></div>
+
  |-  
−
| class=" " | Column1
+
  | 14
−
| class="     " | Column2
 
−
| class=" " | Column3
 
−
| class=" " | Column4
 
−
|- class="odd"
 
−
| class=" " | Row1
 
−
| class="sshl_f " | 5
 
−
| class="sshl_f " | 17
 
−
| class="sshl_f" |
 
−
| class="sshl_f" |
 
−
|- class="even"
 
−
| class=" " | Row2
 
−
| class="sshl_f" | 10
 
−
| class="sshl_f" | 28
 
−
| class="sshl_f" |
 
−
| class="sshl_f" |
 
−
|- class="odd"
 
−
| Row3
 
−
| class="sshl_f" | 4
 
−
| class="sshl_f" | 35
 
−
| class="sshl_f" |
 
−
| class="sshl_f" |
 
−
|- class="even"
 
−
| Row4
 
−
| class="sshl_f" | 8
 
−
| class="sshl_f" | 48
 
−
| class="sshl_f" |
 
−
| class="sshl_f" |
 
−
|- class="odd"
 
−
| class=" " | Row5
 
−
| class=" " | 19
 
−
| class="sshl_f " | 40
 
−
| class="sshl_f" |
 
−
| class="sshl_f" |
 
−
|- class="even"
 
−
| class="sshl_f" | Row6
 
−
| class="sshl_f" | 0.21573734399999997
 
−
| class="sshl_f" |
 
−
| class="sshl_f" |
 
−
|
 
−
|- class="odd"
 
−
| class="sshl_f" | Row7
 
−
| class="sshl_f        " |
 
−
| class="SelectTD" |
 
−
| class="sshl_f" |
 
−
| class="sshl_f" |
 
 
|}
 
|}
 +
{| class="wikitable"
 +
|+ DATA1
 +
|-
 +
| 45
 +
| 65
 +
|}
 +
=FTEST(B1,C2:C3)=NAN
 +
 +
==Related Videos==
 +
 +
{{#ev:youtube|tscL1fzjSTY|280|center|F-Test}}
 +
 +
==See Also==
 +
*[[Manuals/calci/FDIST  | FDIST ]]
 +
*[[Manuals/calci/FINV  | FINV ]]
 +
 +
==References==
 +
[http://en.wikipedia.org/wiki/F-test  F Test]
  
−
<div align="left">[[Image:calci1.gif]]</div></div>
 
−
----
 
−
<div id="8SpaceContent" class="zcontent" align="left"><font size="3"><font face="Times New Roman">''' <font size="3"><font face="Times New Roman">AVEDEV (N1, N2...)</font></font> <font size="3"><font face="Times New Roman">Where N1, N 2 ...   are positive integers.</font></font> '''</font></font></div>
 
−
----
 
−
<div id="5SpaceContent" class="zcontent" align="left">
 
  
−
i.e =FTEST (C1R1:C1R5, C2R1:C2R5) is 0.2157
+
*[[Z_API_Functions | List of Main Z Functions]]
  
−
</div>
+
*[[ Z3 |  Z3 home ]]
−
----
 

Latest revision as of 16:07, 7 August 2018

FTEST(Array1,Array2)


  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2 } are array of data.
    • FTEST(), returns the result of an F-test.

Description

  • This function gives the result of F-test.
  • The F-test is designed to test if two population variances are equal.
  • It does this by comparing the ratio of two variances.
  • So, if the variances are equal, the ratio of the variances will be 1.
  • Let X1,...Xn and Y1,...Ym be independent samples each have a Normal Distribution .
  • It's sample means:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar X=\frac{1}{n} \sum_{i=1}^n Xi} and

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar Y =\frac {1}{m} \sum_{i=1}^m Yi} .
  • The sample variances :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SX^2=\frac{1}{n-1} \sum_{i=1}^n (Xi-\bar X)^2}

and

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SY^2=\frac{1}{m-1} \sum_{i=1}^m (Yi-\bar Y)^2}
  • Then the Test Statistic = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {Sx^2}{Sy^2}} has an F-distribution with 'n−1' and 'm−1' degrees of freedom.
  • In FTEST(Array1,Array2) where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array1} is the data of first array, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2} is the data of second array.
  • The array may be any numbers, names, or references that contains numbers.
  • values are not considered if the array contains any text, logical values or empty cells.

When the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array1} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2} is less than 2 or the variance of the array value is zero, then this function will return the result as error.

ZOS

  • The syntax is to calculate FTEST in ZOS is .
    • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2 } are array of data.
  • For e.g.,FTEST([15,29,30],[62,74,80])
F-Test

Examples

1.

DATA1
15 27 19 32
DATA2
21 12 30 11 
=FTEST(B4:B8,C4:C8)=0.81524906747183

2.

DATA1
5 8 12 45 23
DATA2
10 20 30 40 50 
=FTEST(A1:A5,C1:C5)=0.9583035732212274

3.

DATA1
14 26 37
DATA2
45 82 21 17 
FTEST(B1:B3,C1:C4} = 0.26412211240525474

4.

DATA1
14
DATA1
45 65 
=FTEST(B1,C2:C3)=NAN

Related Videos

F-Test

See Also

References

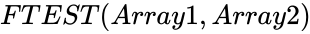F Test


Retrieved from "http://wiki.zcubes.com/index.php?title=Manuals/calci/FTEST&oldid=210938"