Difference between revisions of "Manuals/calci/TTESTUNEQUALVARIANCES"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''TTESTTWOSAMPLESUNEQUALVARIANCES('''Array1, Array2, HypothesizeDiff, Alpha, NewTableFlag) where, '''Array1 '...") |
|||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''TTESTTWOSAMPLESUNEQUALVARIANCES(ar1,ar2,md,alpha,lv)'''</div><br/> |
| + | *<math>ar1 </math> and <math> ar2 </math> are set of values. | ||
| + | *<math>md </math> is the Hypothesized Mean Difference. | ||
| + | *<math> alpha </math> is the significance level. | ||
| + | *<math> lv </math> is the logical value. | ||
| − | + | ==Description== | |
| + | *This function calculating the two Sample for unequal variances determines whether two sample means also distinct. | ||
| + | *We can use this test when both: | ||
| + | *1.the two sample sizes are may are may not be equal; | ||
| + | *2. The means and variances are distinct . | ||
| + | *In <math>TTESTTWOSAMPLESUNEQUALVARIANCES(ar1,ar2,md,alpha,lv)</math>, <math>ar1</math> and <math> ar2 </math> are two arrays of sample values. | ||
| + | *<math> md </math> is the Hypothesized Mean Difference. Suppose md = 0 which indicates that sample means are hypothesized to be equal. | ||
| + | *<math> alpha </math> is the significance level which ranges from 0 to 1. | ||
| + | *<math> lv </math> is the logical value like TRUE or FALSE. | ||
| + | *TRUE is indicating the result will display in new worksheet.Suppose we are omitted the <math>lv</math> value it will consider the value as FALSE. | ||
| + | *The t-statistic of this function calculated by: | ||
| + | <math> t=\frac{\bar{x_1}-\bar{x_2}}{s_{\bar{x_1}-\bar{x_2}}}</math> | ||
| + | where <math>s_{\bar{x_1}-\bar{x_2}}= \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}} </math> | ||
| + | *Here <math> s_1^2</math> and <math> s_2^2</math> are unbiased estimators of the variances of two samples. <math> n_1</math> and <math> n_2</math> are the number of data points in two arrays. <math>s_{\bar{x_1}-\bar{x_2}}</math> is not a pooled variance. | ||
| + | *This function will give the result as error when | ||
| + | 1. any one of the argument is non-numeric. | ||
| + | 2.alpha>1 | ||
| − | + | ==Examples== | |
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C !! D!! E !! F !! G | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 12 || 21 || 9 || 18 || 27 || 37 ||41 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 19 || 8 || 45 || 29 || 14 || 10 || 11 | ||
| + | |} | ||
| − | |||
| − | |||
| − | + | #=TTESTTWOSAMPLESUNEQUALVARIANCES(A1:F1,A2:F2,3,0.5) | |
| − | + | {| class="wikitable" | |
| − | + | |+Result | |
| − | + | |- | |
| − | + | ! !! Variable 1 !! Variable 2 | |
| − | ---- | + | |- |
| − | + | ! Mean | |
| − | + | | 20.666666666666668 || 20.833333333333332 | |
| − | < | + | |- |
| − | + | ! Variance | |
| − | + | | 105.06666666666665 || 196.56666666666666 | |
| − | + | |- | |
| − | + | ! Observations | |
| − | + | | 6 || 6 | |
| − | + | |- | |
| − | + | ! Hypothesized Mean Difference | |
| − | < | + | | 3 |
| − | + | |- | |
| − | + | ! Degree Of Freedom | |
| + | | 9 | ||
| + | |- | ||
| + | ! T- Statistics | ||
| + | | -0.4466201458140038 | ||
| + | |- | ||
| + | ! P(T<=t) One-tail | ||
| + | | 0.3328511748583461 | ||
| + | |- | ||
| + | ! T Critical One-Tail | ||
| + | | 0 | ||
| + | |- | ||
| + | ! P(T<=t) Two-tail | ||
| + | | 0.6657023497166922 | ||
| + | |- | ||
| + | ! T Critical Two-Tail | ||
| + | | 0.7027221467691982 | ||
| + | |} | ||
| − | + | ==Related Videos== | |
| − | |||
| − | |||
| − | + | {{#ev:youtube|L-jfenou5hI|280|center|TTESTUNEQUALVARIANCES}} | |
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/TTEST | TTEST ]] | |
| − | + | *[[Manuals/calci/TDIST | TDIST ]] | |
| − | + | *[[Manuals/calci/TINV | TINV ]] | |
| − | + | *[[Manuals/calci/TTESTEQUALVARIANCES | TTESTEQUALVARIANCES ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==References== | |
| − | + | *[http://en.wikipedia.org/wiki/Student%27s_t-test Student's t-test] | |
Latest revision as of 13:04, 2 July 2015
TTESTTWOSAMPLESUNEQUALVARIANCES(ar1,ar2,md,alpha,lv)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ar1 } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ar2 } are set of values.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle md } is the Hypothesized Mean Difference.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle alpha } is the significance level.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle lv } is the logical value.
Description
- This function calculating the two Sample for unequal variances determines whether two sample means also distinct.
- We can use this test when both:
- 1.the two sample sizes are may are may not be equal;
- 2. The means and variances are distinct .
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle TTESTTWOSAMPLESUNEQUALVARIANCES(ar1,ar2,md,alpha,lv)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ar1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ar2 } are two arrays of sample values.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle md } is the Hypothesized Mean Difference. Suppose md = 0 which indicates that sample means are hypothesized to be equal.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle alpha } is the significance level which ranges from 0 to 1.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle lv } is the logical value like TRUE or FALSE.
- TRUE is indicating the result will display in new worksheet.Suppose we are omitted the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle lv} value it will consider the value as FALSE.
- The t-statistic of this function calculated by:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=\frac{\bar{x_1}-\bar{x_2}}{s_{\bar{x_1}-\bar{x_2}}}} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{\bar{x_1}-\bar{x_2}}= \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}} }
- Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_1^2} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_2^2} are unbiased estimators of the variances of two samples. and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_2} are the number of data points in two arrays. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{\bar{x_1}-\bar{x_2}}} is not a pooled variance.
- This function will give the result as error when
1. any one of the argument is non-numeric.
2.alpha>1
Examples
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | 12 | 21 | 9 | 18 | 27 | 37 | 41 |
| 2 | 19 | 8 | 45 | 29 | 14 | 10 | 11 |
- =TTESTTWOSAMPLESUNEQUALVARIANCES(A1:F1,A2:F2,3,0.5)
| Variable 1 | Variable 2 | |
|---|---|---|
| Mean | 20.666666666666668 | 20.833333333333332 |
| Variance | 105.06666666666665 | 196.56666666666666 |
| Observations | 6 | 6 |
| Hypothesized Mean Difference | 3 | |
| Degree Of Freedom | 9 | |
| T- Statistics | -0.4466201458140038 | |
| P(T<=t) One-tail | 0.3328511748583461 | |
| T Critical One-Tail | 0 | |
| P(T<=t) Two-tail | 0.6657023497166922 | |
| T Critical Two-Tail | 0.7027221467691982 |
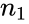 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_2}
are the number of data points in two arrays. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{\bar{x_1}-\bar{x_2}}}
is not a pooled variance.
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_2}
are the number of data points in two arrays. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{\bar{x_1}-\bar{x_2}}}
is not a pooled variance.