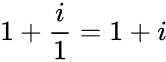Difference between revisions of "Manuals/calci/IMDIV"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*<math>z1,z2</math> are the two complex numbers in the form of <math>z1=a+ib</math> and <math>z2=c+id</math>, where <math>a,b,c</math> & <math>d</math> are real numbers <math>i</math> is the imaginary unit, <math>i=\sqrt{-1}</math>. | *<math>z1,z2</math> are the two complex numbers in the form of <math>z1=a+ib</math> and <math>z2=c+id</math>, where <math>a,b,c</math> & <math>d</math> are real numbers <math>i</math> is the imaginary unit, <math>i=\sqrt{-1}</math>. | ||
*To do the division of complex number we have follow the steps: | *To do the division of complex number we have follow the steps: | ||
| − | step 1: | + | step 1: Write the complex number in the fraction form. |
| − | step 2: | + | step 2: Find the conjugate of the denominator. |
| − | step 3: | + | step 3: Multiply the numerator and denominator with conjugate. |
:<math>IMDIV(z1,z2) = \frac{a+ib}{c+id} = \frac{a+ib}{c+id}*\frac{c-id}{c-id} =\frac{ac+bd}{c^2+d^2}+\frac{(bc-ad)i}{(c^2+d^2)}</math> | :<math>IMDIV(z1,z2) = \frac{a+ib}{c+id} = \frac{a+ib}{c+id}*\frac{c-id}{c-id} =\frac{ac+bd}{c^2+d^2}+\frac{(bc-ad)i}{(c^2+d^2)}</math> | ||
Revision as of 00:57, 26 November 2013
IMDIV(z1,z2)
- and are complex numbers.
Description
- This function gives the division of two complex numbers.
- This function used to remove the (imaginary unit) from the denominator.
- are the two complex numbers in the form of and , where & are real numbers is the imaginary unit, .
- To do the division of complex number we have follow the steps:
step 1: Write the complex number in the fraction form. step 2: Find the conjugate of the denominator. step 3: Multiply the numerator and denominator with conjugate.
Examples
- IMDIV("4+2i","3-i") = = (because ) =
- IMDIV("3-5i,2-6i") = 0.9+0.2i
- IMDIV("5","2+3i") = 0.769-1.153i
- IMDIV("1+i","2") = 0.5+0.5i
See Also
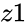 and
and 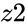 are complex numbers.
are complex numbers. (imaginary unit) from the denominator.
(imaginary unit) from the denominator.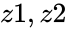 are the two complex numbers in the form of
are the two complex numbers in the form of  and
and 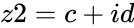 , where
, where 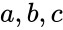 &
& 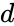 are real numbers
are real numbers 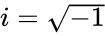 .
.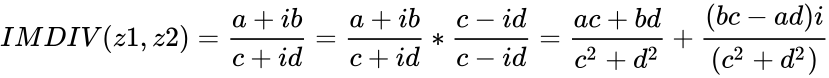
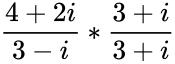 =
= 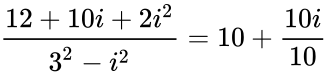 (because
(because 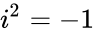 ) =
) =