Difference between revisions of "Manuals/calci/TTESTUNEQUALVARIANCES"
Jump to navigation
Jump to search
| Line 80: | Line 80: | ||
*[[Manuals/calci/TINV | TINV ]] | *[[Manuals/calci/TINV | TINV ]] | ||
*[[Manuals/calci/TTESTEQUALVARIANCES | TTESTEQUALVARIANCES ]] | *[[Manuals/calci/TTESTEQUALVARIANCES | TTESTEQUALVARIANCES ]] | ||
| − | |||
==References== | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Student%27s_t-test Student's t-test] | ||
Revision as of 13:05, 11 May 2015
TTESTTWOSAMPLESUNEQUALVARIANCES(ar1,ar2,md,alpha,lv)
- and are set of values.
- is the Hypothesized Mean Difference.
- is the significance level.
- is the logical value.
Description
- This function calculating the two Sample for unequal variances determines whether two sample means also distinct.
- We can use this test when both:
- 1.the two sample sizes are may are may not be equal;
- 2. The means and variances are distinct .
- In , and are two arrays of sample values.
- is the Hypothesized Mean Difference. Suppose md = 0 which indicates that sample means are hypothesized to be equal.
- is the significance level which ranges from 0 to 1.
- is the logical value like TRUE or FALSE.
- TRUE is indicating the result will display in new worksheet.Suppose we are omitted the value it will consider the value as FALSE.
- The t-statistic of this function calculated by:
where
- Here and are unbiased estimators of the variances of two samples. and are the number of data points in two arrays. is not a pooled variance.
- This function will give the result as error when
1. any one of the argument is non-numeric.
2.alpha>1
Examples
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | 12 | 21 | 9 | 18 | 27 | 37 | 41 |
| 2 | 19 | 8 | 45 | 29 | 14 | 10 | 11 |
- =TTESTTWOSAMPLESUNEQUALVARIANCES(A1:F1,A2:F2,3,0.5)
| Variable 1 | Variable 2 | |
|---|---|---|
| Mean | 20.666666666666668 | 20.833333333333332 |
| Variance | 105.06666666666665 | 196.56666666666666 |
| Observations | 6 | 6 |
| Hypothesized Mean Difference | 3 | |
| Degree Of Freedom | 9 | |
| T- Statistics | -0.4466201458140038 | |
| P(T<=t) One-tail | 0.3328511748583461 | |
| T Critical One-Tail | 0 | |
| P(T<=t) Two-tail | 0.6657023497166922 | |
| T Critical Two-Tail | 0.7027221467691982 |
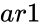 and
and 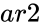 are set of values.
are set of values.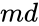 is the Hypothesized Mean Difference.
is the Hypothesized Mean Difference.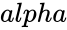 is the significance level.
is the significance level. is the logical value.
is the logical value.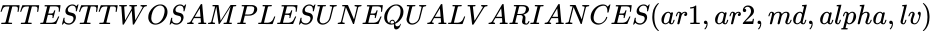 ,
, 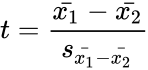 where
where 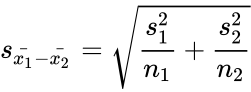
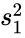 and
and 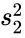 are unbiased estimators of the variances of two samples.
are unbiased estimators of the variances of two samples. 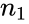 and
and 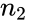 are the number of data points in two arrays.
are the number of data points in two arrays. 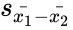 is not a pooled variance.
is not a pooled variance.