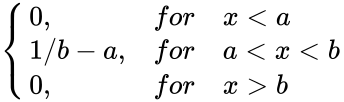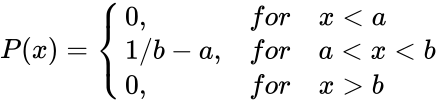Difference between revisions of "Manuals/calci/UNIFORM"
Jump to navigation
Jump to search
| Line 11: | Line 11: | ||
*The Probability Density Function of the uniform distribution for the interval(a,b) is given by: | *The Probability Density Function of the uniform distribution for the interval(a,b) is given by: | ||
P(x)=<math>\begin{cases} 0, &for &x<a \\ | P(x)=<math>\begin{cases} 0, &for &x<a \\ | ||
| − | 1/b-a, &for &a<x \\ | + | 1/b-a, &for &a<x<b \\ |
0, &for &x>b \\ | 0, &for &x>b \\ | ||
\end{cases}</math> | \end{cases}</math> | ||
Revision as of 00:26, 11 February 2014
UNIFORMDISTRIBUTED(x,ll,ul)
- is the value of the function.
- is the lower limit.
- is the upper limit of the function.
Description
- This function gives the probability of the uniform distribution.
- Uniform distribution is a symmetric probability distribution.
- It is also called rectangular distribution.
- In , is the numeric value to find the probability of the distribution, is the lower limit value and is the upper limit value.
- The Probability Density Function of the uniform distribution for the interval(a,b) is given by:
P(x)=
equation
- The Lucas numbers are defined by:
Examples
- UNIFORMDISTRIBUTED(4,2,3) = 4030484680552036 2.6280935418326408 2.2810050058178604 2.97846262995153679
- UNIFORMDISTRIBUTED(5,3,6) = 5.522187389200553 3.566177821950987 5.04674904467538 5.301322509767488 4.9094569575972855
 is the value of the function.
is the value of the function. is the lower limit.
is the lower limit. is the upper limit of the function.
is the upper limit of the function.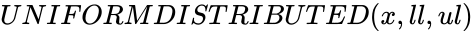 ,
,