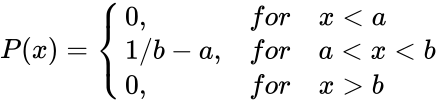Difference between revisions of "Manuals/calci/UNIFORM"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
*In <math>UNIFORMDISTRIBUTED(x,ll,ul)</math> ,<math> x </math> is the numeric value to find the probability of the distribution, <math>ll </math> is the lower limit value and <math> ul </math> is the upper limit value. | *In <math>UNIFORMDISTRIBUTED(x,ll,ul)</math> ,<math> x </math> is the numeric value to find the probability of the distribution, <math>ll </math> is the lower limit value and <math> ul </math> is the upper limit value. | ||
*The Probability Density Function of the uniform distribution for the interval(a,b) is given by: | *The Probability Density Function of the uniform distribution for the interval(a,b) is given by: | ||
| − | P(x)=<math>\begin{cases} 0, &for &x<a \\ | + | P(x)=<math>\begin{cases} 0, &for & x < a \\ |
| − | 1/b-a, &for &a< | + | 1/b-a, &for & a < x < b \\ |
| − | 0, &for &x>b | + | 0, &for & x > b |
\end{cases}</math> | \end{cases}</math> | ||
Revision as of 00:28, 11 February 2014
UNIFORMDISTRIBUTED(x,ll,ul)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } is the value of the function.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ll } is the lower limit.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ul } is the upper limit of the function.
Description
- This function gives the probability of the uniform distribution.
- Uniform distribution is a symmetric probability distribution.
- It is also called rectangular distribution.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UNIFORMDISTRIBUTED(x,ll,ul)} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } is the numeric value to find the probability of the distribution, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ll } is the lower limit value and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ul } is the upper limit value.
- The Probability Density Function of the uniform distribution for the interval(a,b) is given by:
P(x)=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} 0, &for & x < a \\ 1/b-a, &for & a < x < b \\ 0, &for & x > b \end{cases}}
equation
- The Lucas numbers are defined by: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)=\begin{cases} 0, &for &x<a \\ 1/b-a, &for &a<x<b \\ 0, &for &x>b \end{cases}}
Examples
- UNIFORMDISTRIBUTED(4,2,3) = 4030484680552036 2.6280935418326408 2.2810050058178604 2.97846262995153679
- UNIFORMDISTRIBUTED(5,3,6) = 5.522187389200553 3.566177821950987 5.04674904467538 5.301322509767488 4.9094569575972855