Difference between revisions of "Manuals/calci/EIGENVALUES"
Jump to navigation
Jump to search
| Line 54: | Line 54: | ||
|} | |} | ||
=EIGENVALUES(A1:B2) | =EIGENVALUES(A1:B2) | ||
| − | {| | + | {| border="1" cellpadding="5" cellspacing="0" |
| − | |||
|- | |- | ||
| − | | -13.862780491200214 || 7.8627804912002155 | + | | |
| + | -13.862780491200214 | ||
| + | || | ||
| + | 7.8627804912002155 | ||
|- | |- | ||
| − | | 0.3031213645114406 0.9025310769284506 | + | | |
| − | || -0.9529519601620652 0.43062472662211493 | + | 0.3031213645114406 0.9025310769284506 |
| + | || | ||
| + | -0.9529519601620652 0.43062472662211493 | ||
|} | |} | ||
Revision as of 05:03, 5 September 2017
EIGENVALUES (Matrix)
- is the array of numeric elements.
Description
- This function shows the Eigen value of the given matrix.
- In , is any matrix values.
- In linear algebra,an eigen vector or characteristic vector of a linear transformation is a non-zero vector whose direction does not change when that linear transformation is applied to it.
- Let A be a linear transformation represented by a matrix A.
- Let A is an nxn matrix,v is a non zero nx1 vector and is a scalar which may be either real or complex.
- Any value of for which this equation has a solution is known as an eigenvalue of the matrix A.
- It is sometimes also called the characteristic value.
- The vector, v, which corresponds to this value is called an eigenvector.
- The eigenvalue problem can be rewritten as .
- If v is non-zero, this equation will only have a solution if .
- This equation is called the characteristic equation of A, and is an nth order polynomial in with n roots.
- These roots are called the eigenvalues of A.
Examples
| A | B | C | |
|---|---|---|---|
| 1 | 3 | 7 | 5 |
| 2 | 10 | 12 | 8 |
| 3 | 6 | 8 | 14 |
=EIGENVALUES(A1:C3)
-2.018987498930866 25.303239119591886 5.715748379338994 | ||
| -0.8195524172935329 0.3557792393359474 0.2128903683040517 | 0.5726193656991498 0.663334322125492 0.6212592923173481 | 0.02099755544415341 0.6583378387635402 -0.7541316747045657 |
| A | B | |
|---|---|---|
| 1 | 5 | 6 |
| 2 | 9 | -11 |
=EIGENVALUES(A1:B2)
-13.862780491200214 |
7.8627804912002155 |
0.3031213645114406 0.9025310769284506 |
-0.9529519601620652 0.43062472662211493 |
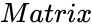 is the array of numeric elements.
is the array of numeric elements.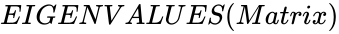 ,
,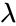 is a scalar which may be either real or complex.
is a scalar which may be either real or complex.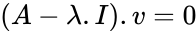 .
. .
.