Difference between revisions of "Manuals/calci/BETADIST"
Jump to navigation
Jump to search
| Line 16: | Line 16: | ||
<math>f(x)=\frac{x^{\alpha-1}(1-x)^{ \beta-1}}{B(\alpha,\beta)},</math> where <math>0 \le x \le 1</math>; <math>\alpha,\beta >0 </math> and <math>B(\alpha,\beta)</math> is the Beta function. | <math>f(x)=\frac{x^{\alpha-1}(1-x)^{ \beta-1}}{B(\alpha,\beta)},</math> where <math>0 \le x \le 1</math>; <math>\alpha,\beta >0 </math> and <math>B(\alpha,\beta)</math> is the Beta function. | ||
*The formula for the Cumulative Beta Distribution is called the Incomplete Beta function ratio and it is denoted by <math>I_x</math> and is defined as : | *The formula for the Cumulative Beta Distribution is called the Incomplete Beta function ratio and it is denoted by <math>I_x</math> and is defined as : | ||
| − | <math>F(x)=I_x(\alpha,\beta)</math>=<math>\int_{0}^{x} | + | <math>F(x)=I_x(\alpha,\beta)</math>=<math>\int_{0}^{x}f(x)=\frac{t^{\alpha-1}(1-t)^{ \beta-1}dt}{B(\alpha,\beta)}</math>, where <math>0 \le t \le 1</math> ; <math>\alpha,\beta>0</math> and <math>B(\alpha,\beta)</math> is the Beta function. |
*This function will give the result as error when | *This function will give the result as error when | ||
1.Any one of the arguments are non-numeric. | 1.Any one of the arguments are non-numeric. | ||
Revision as of 15:23, 19 January 2018
BETADIST(x,alpha,beta,a,b)
- is the value between and
- alpha and beta are the value of the shape parameter
- & the lower and upper limit to the interval of .
Description
- This function gives the Cumulative Beta Probability Density function.
- The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by and .
- The Beta Distribution is also known as the Beta Distribution of the first kind.
- In , is the value between and .
- alpha is the value of the shape parameter.
- beta is the value of the shape parameter
- and (optional) are the Lower and Upper limit to the interval of .
- Normally lies between the limit and , suppose when we are omitting and value, by default value with in 0 and 1.
- The Probability Density Function of the beta distribution is:
where ; and is the Beta function.
- The formula for the Cumulative Beta Distribution is called the Incomplete Beta function ratio and it is denoted by and is defined as :
=, where ; and is the Beta function.
- This function will give the result as error when
1.Any one of the arguments are non-numeric. 2. or 3. ,, or
- we are not mentioning the limit values and ,
- By default it will consider the Standard Cumulative Beta Distribution, a = 0 and b = 1.
Failed to parse (syntax error): {\displaystyle t^{\alpha−1} }
Failed to parse (syntax error): {\displaystyle {x^{\alpha-1}}
ZOS
- The syntax is to calculate BEATDIST in ZOS is .
- is the value between LowerBound and UpperBound
- and are the value of the shape parameter.
- For e.g.,BETADIST(11..13,3,5,8,14)
- BETADIST(33..35,5..6,10..11,30,40)
Examples
- =BETADIST(0.4,8,10) = 0.35949234293309396
- =BETADIST(3,5,9,2,6) = 0.20603810250759128
- =BETADIST(9,4,2,8,11) = 0.04526748971193415
- =BETADIST(5,-1,-2,4,7) = #ERROR
Related Videos
See Also
References
 is the value between
is the value between  and
and 
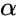 and
and 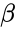 .
.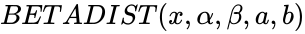 ,
, 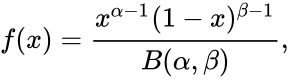 where
where  ;
; 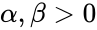 and
and 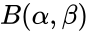 is the Beta function.
is the Beta function.
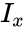 and is defined as :
and is defined as :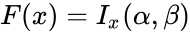 =
=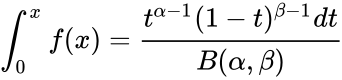 , where
, where 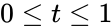 ;
; 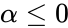 or
or 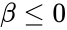 3.
3.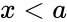 ,
,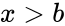 , or
, or 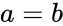
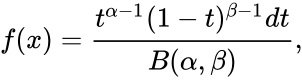
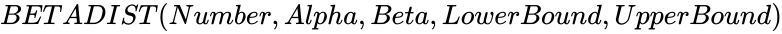 .
.
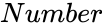 is the value between LowerBound and UpperBound
is the value between LowerBound and UpperBound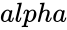 and
and  are the value of the shape parameter.
are the value of the shape parameter.