Difference between revisions of "Manuals/calci/MAKECOMPLEXIPLUS"
Jump to navigation
Jump to search
| Line 32: | Line 32: | ||
#=MAKECOMPLEXIPLUS(1,-10,"j") = 1-j10 | #=MAKECOMPLEXIPLUS(1,-10,"j") = 1-j10 | ||
#=MAKECOMPLEXIPLUS(1,0) = 1+i0 | #=MAKECOMPLEXIPLUS(1,0) = 1+i0 | ||
| − | #=MAKECOMPLEXIPLUS(1..3,-5) = 1- | + | #=MAKECOMPLEXIPLUS(1..3,-5) |
| + | {| class="wikitable" | ||
| + | |- class="even" | ||
| + | !Real | ||
| + | !Imaginary | ||
| + | !MAKECOMPLEXIPLUS | ||
| + | |- class="odd" | ||
| + | |1 | ||
| + | | -5 | ||
| + | |1-5ⅈ | ||
| + | |- class="even" | ||
| + | |2 | ||
| + | | -5 | ||
| + | |2-5ⅈ | ||
| + | |- class="odd" | ||
| + | |3 | ||
| + | | -5 | ||
| + | |3-5ⅈ | ||
| + | |} | ||
==Related Videos== | ==Related Videos== | ||
Latest revision as of 06:48, 29 September 2021
MAKECOMPLEXIPLUS (Real,Imaginary)
- is the real part of the complex number.
- is the imaginary part of the complex number.
Description
- MAKECOMPLEXIPLUS function converts the imaginary coefficient of a complex number into 'positive' coefficient.
- A complex number is a combination of a real and an imaginary number.
- A number which is positive or negative, rational or irrational or decimals are called real numbers.
- An Imaginary number is a number that when squring it gives a negative result.
- For e.g. . Because a negative times a negative is positive.
- A complex number is a number is in the form , where and are real numbers and is the imaginary unit. Where
- To mention and , we must use the lower case only
- In a complex number real part is denoted by & imaginary part is denoted by .
- MAKECOMPLEXIPLUS returns the error value, when and are non-numeric.
- A Complex number whose real part is zero is said to be purely imaginary.
- A Complex number whose imaginary part is zero is a real number. In that cases we have to assign '0' for that part.
- =MAKECOMPLEXIPLUS (5,2) gives
- =MAKECOMPLEXIPLUS (5,2,["j"]) gives
ZOS
- The syntax is to calculate MAKECOMPLEXIPLUS in ZOS is
- is the real part.
- is the imaginary part.
Examples
- =MAKECOMPLEXIPLUS(4,-5) = 4-i5
- =MAKECOMPLEXIPLUS(4,5) = 4+i5
- =MAKECOMPLEXIPLUS(1,-10,"j") = 1-j10
- =MAKECOMPLEXIPLUS(1,0) = 1+i0
- =MAKECOMPLEXIPLUS(1..3,-5)
| Real | Imaginary | MAKECOMPLEXIPLUS |
|---|---|---|
| 1 | -5 | 1-5ⅈ |
| 2 | -5 | 2-5ⅈ |
| 3 | -5 | 3-5ⅈ |
Related Videos
See Also
References
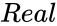 is the real part of the complex number.
is the real part of the complex number.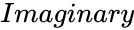 is the imaginary part of the complex number.
is the imaginary part of the complex number.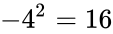 . Because a negative times a negative is positive.
. Because a negative times a negative is positive.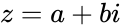 , where
, where  and
and  are real numbers and
are real numbers and  is the imaginary unit. Where
is the imaginary unit. Where 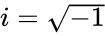
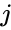 , we must use the lower case only
, we must use the lower case only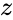 real part is denoted by
real part is denoted by 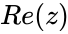 & imaginary part is denoted by
& imaginary part is denoted by 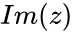 .
.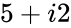
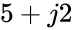
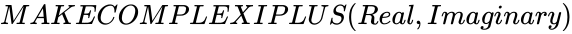
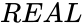 is the real part.
is the real part.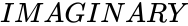 is the imaginary part.
is the imaginary part.