Difference between revisions of "Manuals/calci/IMCONJUGATE"
Jump to navigation
Jump to search
| Line 17: | Line 17: | ||
|- class="even" | |- class="even" | ||
!Equation | !Equation | ||
| − | + | ! a | |
| − | + | ! bi | |
| − | + | ! Result | |
| − | + | ! Result | |
|- class="odd" | |- class="odd" | ||
|=IMCONJUGATE("3+4i") | |=IMCONJUGATE("3+4i") | ||
Revision as of 03:55, 25 November 2013
IMCONJUGATE(z)
- where is the complex number.
Description
- This function gives the conjugate of a complex number.
- The complex number , then and it is denoted by or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^*} .
- So complex number and complex conjugate both also having same real number and imaginary number with
the equal magnitude and opposite sign of a imaginary number.Also
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=\bar{z}} if imaginary number is '0' and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=\bar{\bar{z}} = z}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\bar{z}|=|z|} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z|^2 = z.\bar{z} = \bar{z}.z}
- Real part (a)=z+z(bar)/2
- Imaginary part(b)=z-z(bar)/2i.We can use COMPLEX function to convert the real and imginary coefficients to a complex number.
Examples
| Equation | a | bi | Result | Result |
|---|---|---|---|---|
| =IMCONJUGATE("3+4i") | 3 | 4i | 3+4i | 3-4i |
| =IMCONJUGATE("6-7i") | 6 | -7i | 6+7i | |
| =IMCONJUGATE("8j") | 0 | 8j | 0+8j | 0-8j |
| =IMCONJUGATE("2") | 2 | 0 | 2+0i | |
| =IMCONJUGATE("5+0i") | 5 | 0i | 5+0i |
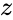 is the complex number.
is the complex number.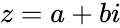 , then
, then 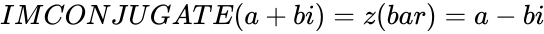 and it is denoted by
and it is denoted by 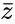 or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^*}
.
or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^*}
.