Difference between revisions of "Manuals/calci/IMPOWER"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*DeMoivre's Theorem is a generalized formula to compute powers of a complex number in it's polar form. | *DeMoivre's Theorem is a generalized formula to compute powers of a complex number in it's polar form. | ||
*i'is the imaginary unit, <math>i=\sqrt{-1}</math> | *i'is the imaginary unit, <math>i=\sqrt{-1}</math> | ||
| − | *Then the power of a complex number is defined by <math>(z)^n=(x+iy)^n=r^n*e^{ | + | *Then the power of a complex number is defined by <math>(z)^n=(x+iy)^n=r^n*e^{in\theta}=r^n(cosn\theta+isinn\theta)</math> where <math>r=\sqrt{x^2+y^2}</math>. and <math>\theta=tan^-1(y/x)</math>, <math>\theta∈(-\pi,\pi]</math>. |
*This formula is called DeMoivre's theorem of complex numbers. | *This formula is called DeMoivre's theorem of complex numbers. | ||
| − | *We can use [[Manuals/calci/COMPLEX| COMPLEX]] function to convert | + | *We can use [[Manuals/calci/COMPLEX| COMPLEX]] function to convert real and imaginary number in to a complex number. |
| − | *In IMPOWER(z,n), n can be integer, fractional or negative. | + | *In IMPOWER(z,n), <math>n</math> can be integer, fractional or negative. |
| − | * | + | *If <math>n</math> is non-numeric, function will return error value. |
==Examples== | ==Examples== | ||
Revision as of 22:42, 19 December 2013
IMPOWER(z,n)
- is the complex number is of the form
- is the power value.
Description
- This function gives the value of powers of complex number.
- DeMoivre's Theorem is a generalized formula to compute powers of a complex number in it's polar form.
- i'is the imaginary unit,
- Then the power of a complex number is defined by where . and , Failed to parse (syntax error): {\displaystyle \theta∈(-\pi,\pi]} .
- This formula is called DeMoivre's theorem of complex numbers.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
- In IMPOWER(z,n), can be integer, fractional or negative.
- If is non-numeric, function will return error value.
Examples
- IMPOWER("4+5i",3)=-235.99999+115i
- IMPOWER("9-7i",4)=-14852-8063.999999i
- IMPOWER("6",9)=10077696
- IMPOWER("i",10)=-1+6.1257422745431E-16i
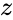 is the complex number is of the form
is the complex number is of the form 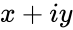
 is the power value.
is the power value.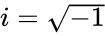
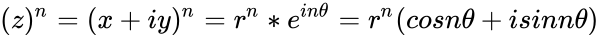 where
where 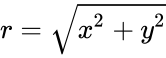 . and
. and 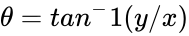 , Failed to parse (syntax error): {\displaystyle \theta∈(-\pi,\pi]}
.
, Failed to parse (syntax error): {\displaystyle \theta∈(-\pi,\pi]}
.