Difference between revisions of "Manuals/calci/TINV"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font color="#484848"><font face="Arial, sans-serif"><font size="2">'''TINV'''</font></font></font><font color="#4848...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''TINV(prob,df) '''</div><br/> |
| + | *<math>prob </math> is the probability value for the two tailed t-distribution. | ||
| + | *<math> df </math> is the degrees of freedom. | ||
| − | |||
| − | + | ==Description== | |
| + | *This function gives the t value of the t-distribution. | ||
| + | *This function is called the inverse function of the t-distribution. | ||
| + | *In <math> TINV(prob,df), prob </math> is the probability value related with the two tailed distribution and <math> df </math> is the number of degrees of freedom which is characterize the distribution. | ||
| + | *i.e., This function is the inverse value of <math> TDIST(x,df,2)</math>. | ||
| + | *Suppose we want to find the inverse value os one tailed distribution, then we have to multiply 2 with the prob value. | ||
| + | *For e.g., TINV(0.078,20)=1.857683 which is the inverse value of two tailed t-distribution. | ||
| + | *TINV(2*0.078,20)=1.474181542 which is the inverse value of one tailed t-distribution. | ||
| + | *Suppose df value is decimal then it is converted in to integers. | ||
| + | *If <math>TDIST(x,df,t)=prob </math>, then <math> TINV(prob,df)=x</math> for the two tailed t-distribution. | ||
| + | *<math> TINV </math> using the iterating method to find the value of <math> x </math>. | ||
| + | *Suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
| + | *This function will give the result as error when | ||
| + | 1.Any one of the argument is nonnumeric. | ||
| + | 2.prob<0 or prob>1 or df<1. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Examples== | |
| − | * | + | #TINV(0.0742,55)=1.820015422 |
| + | #TINV(2*0.0371,55)=1.820015422 | ||
| + | #TINV(0.65482,29) = 0.451735616 | ||
| + | #TINV(0.5,5)=0.726686844 | ||
| + | |||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/TTEST | TTEST]] | |
| − | + | *[[Manuals/calci/TDIST | TDIST ]] | |
| − | |||
| − | + | ==References== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 23:46, 26 January 2014
TINV(prob,df)
- is the probability value for the two tailed t-distribution.
- is the degrees of freedom.
is the probability value for the two tailed t-distribution.
is the degrees of freedom.
Description
- This function gives the t value of the t-distribution.
- This function is called the inverse function of the t-distribution.
- In is the probability value related with the two tailed distribution and is the number of degrees of freedom which is characterize the distribution.
- i.e., This function is the inverse value of .
- Suppose we want to find the inverse value os one tailed distribution, then we have to multiply 2 with the prob value.
- For e.g., TINV(0.078,20)=1.857683 which is the inverse value of two tailed t-distribution.
- TINV(2*0.078,20)=1.474181542 which is the inverse value of one tailed t-distribution.
- Suppose df value is decimal then it is converted in to integers.
- If , then for the two tailed t-distribution.
- using the iterating method to find the value of .
- Suppose the iteration has not converged after 100 searches, then the function gives the error result.
- This function will give the result as error when
is the probability value related with the two tailed distribution and 
.
, then 
for the two tailed t-distribution.
using the iterating method to find the value of 
. 1.Any one of the argument is nonnumeric.
2.prob<0 or prob>1 or df<1.
Examples
- TINV(0.0742,55)=1.820015422
- TINV(2*0.0371,55)=1.820015422
- TINV(0.65482,29) = 0.451735616
- TINV(0.5,5)=0.726686844
See Also
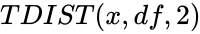