Difference between revisions of "Manuals/calci/TTESTUNEQUALVARIANCES"
Jump to navigation
Jump to search
| Line 12: | Line 12: | ||
*2. The means and variances are distinct . | *2. The means and variances are distinct . | ||
*In <math>TTESTTWOSAMPLESUNEQUALVARIANCES(ar1,ar2,md,alpha,lv), ar1</math> and <math> ar2 </math> are two arrays of sample values. | *In <math>TTESTTWOSAMPLESUNEQUALVARIANCES(ar1,ar2,md,alpha,lv), ar1</math> and <math> ar2 </math> are two arrays of sample values. | ||
| − | *<math> md </math> is the Hypothesized Mean Difference .Suppose md=0 which indicates that sample means are hypothesized to be equal. | + | *<math> md </math> is the Hypothesized Mean Difference .Suppose md = 0 which indicates that sample means are hypothesized to be equal. |
*<math> alpha </math> is the significance level which ranges from 0 to 1. | *<math> alpha </math> is the significance level which ranges from 0 to 1. | ||
*<math> lv </math> is the logical value like TRUE or FALSE. | *<math> lv </math> is the logical value like TRUE or FALSE. | ||
*TRUE is indicating the result will display in new worksheet.Suppose we are omitted the lv value it will consider the value as FALSE. | *TRUE is indicating the result will display in new worksheet.Suppose we are omitted the lv value it will consider the value as FALSE. | ||
*The t statistic of this function calculated by: | *The t statistic of this function calculated by: | ||
| − | <math> t=\frac{\bar{ | + | <math> t=\frac{\bar{x_1}-\bar{x_2}}{s_{\bar{x_1}-\bar{x_2}}}</math> where <math>s_{\bar{x_1}-\bar{x_2}}= \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}} </math> |
| − | *Here <math> s_1^2</math> and <math> s_2^2</math> are unbiased estimators of the variances of two samples. | + | *Here <math> s_1^2</math> and <math> s_2^2</math> are unbiased estimators of the variances of two samples. <math> n_1</math> and <math> n_2</math> are the number of data points in two arrays . <math>s_{\bar{x_1}-\bar{x_2}} is not a pooled variance. |
*This function will give the result as error when | *This function will give the result as error when | ||
| − | 1. any one of | + | 1. any one of the argument is non-numeric. |
2.alpha>1 | 2.alpha>1 | ||
Revision as of 23:40, 3 February 2014
TTESTTWOSAMPLESUNEQUALVARIANCES(ar1,ar2,md,alpha,lv)
- and are set of values.
- is the Hypothesized Mean Difference.
- is the significance level.
- is the logical value.
Description
- This function calculating the two Sample for unequal variances determines whether two sample means also distinct.
- We can use this test when both:
- 1.the two sample sizes are may are may not be equal;
- 2. The means and variances are distinct .
- In and are two arrays of sample values.
- is the Hypothesized Mean Difference .Suppose md = 0 which indicates that sample means are hypothesized to be equal.
- is the significance level which ranges from 0 to 1.
- is the logical value like TRUE or FALSE.
- TRUE is indicating the result will display in new worksheet.Suppose we are omitted the lv value it will consider the value as FALSE.
- The t statistic of this function calculated by:
where
- Here and are unbiased estimators of the variances of two samples. and are the number of data points in two arrays . <math>s_{\bar{x_1}-\bar{x_2}} is not a pooled variance.
- This function will give the result as error when
1. any one of the argument is non-numeric.
2.alpha>1
Examples
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | 12 | 21 | 9 | 18 | 27 | 37 | 41 |
| 2 | 19 | 8 | 45 | 29 | 14 | 10 | 11 |
- =TTESTSAMPLESEQUALVARIANCES(A1:F1,A2:F2,0.5)
See Also
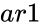 and
and 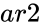 are set of values.
are set of values.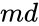 is the Hypothesized Mean Difference.
is the Hypothesized Mean Difference.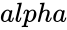 is the significance level.
is the significance level. is the logical value.
is the logical value.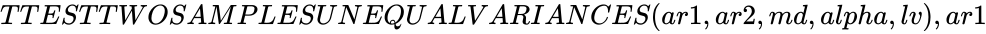 and
and 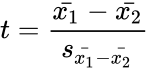 where
where 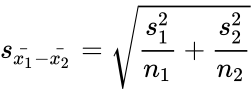
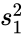 and
and 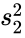 are unbiased estimators of the variances of two samples.
are unbiased estimators of the variances of two samples. 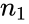 and
and 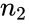 are the number of data points in two arrays . <math>s_{\bar{x_1}-\bar{x_2}} is not a pooled variance.
are the number of data points in two arrays . <math>s_{\bar{x_1}-\bar{x_2}} is not a pooled variance.