Difference between revisions of "Manuals/calci/IMEXP"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''IMEXP( | + | <div style="font-size:30px">'''IMEXP(ComplexNumber)'''</div><br/> |
| − | * | + | *<math>ComplexNumber</math> is of the form a+bi. |
| + | |||
==Description== | ==Description== | ||
| + | |||
*This function gives the exponential of a complex number. | *This function gives the exponential of a complex number. | ||
| − | *In <math>IMEXP( | + | *In <math>IMEXP(ComplexNumber)</math>, <math>ComplexNumber</math> is of the form <math>x+iy</math>, <math>x</math>&<math>y</math> are real numbers & <math>i</math> is the imaginary unit. <math>i=\sqrt{-1}</math>. |
*Euler's formula states that <math>e^{ix}= cosx+isinx</math>, for any real number <math>x</math> and <math>e</math> is the base of the natural logarithm. | *Euler's formula states that <math>e^{ix}= cosx+isinx</math>, for any real number <math>x</math> and <math>e</math> is the base of the natural logarithm. | ||
| − | *The approximate value of the constant e=2.718281828459045 and it is equal to <math>e^1</math>. | + | *The approximate value of the constant e=2.718281828459045 and it is equal to <math>e^1</math>. |
| + | *Let z be the Complex Number.Then the exponential of a complex number is : <math>IMEXP(z) = e^z = e^{x+iy} = e^{x}.e^{iy} = e^{x}.(cosy+isiny)=e^x.cosy+ie^x.siny</math>. | ||
| + | *Here Sin and Cos are trignometric functions. y is angle value in radians. | ||
*When imaginary part is '0', it will give the exponent value of the real number. i.e <math>IMEXP(z) = EXP(z)</math> when imaginary number <math>iy</math> is '0'. | *When imaginary part is '0', it will give the exponent value of the real number. i.e <math>IMEXP(z) = EXP(z)</math> when imaginary number <math>iy</math> is '0'. | ||
| − | *We can use COMPLEX function to convert the real and imaginary coefficients to a complex number. | + | *The Complex exponential function is denoted by "'''cis(x)'''"(Cosine plus iSine) |
| + | *We can use [[Manuals/calci/COMPLEX | COMPLEX ]] function to convert the real and imaginary coefficients to a complex number. | ||
==Examples== | ==Examples== | ||
| + | |||
#=IMEXP("2+3i") = -7.315110094901102+1.0427436562359i | #=IMEXP("2+3i") = -7.315110094901102+1.0427436562359i | ||
#=IMEXP("4-5i") = 15.4874305606508+52.355491418482i | #=IMEXP("4-5i") = 15.4874305606508+52.355491418482i | ||
| Line 15: | Line 21: | ||
#=IMEXP("2i") = -0.416146836547142+0.909297426825682i | #=IMEXP("2i") = -0.416146836547142+0.909297426825682i | ||
#=IMEXP("0") = 1 and IMEXP("0i") = 1 | #=IMEXP("0") = 1 and IMEXP("0i") = 1 | ||
| + | |||
| + | ==ZOS Section== | ||
| + | *The syntax is to calculate IMEXP in ZOS is <math>IMEXP(ComplexNumber)</math>. | ||
| + | **<math>ComplexNumber</math> is of the form a+bi. | ||
| + | *For e.g., | ||
==See Also== | ==See Also== | ||
Revision as of 00:42, 24 April 2014
IMEXP(ComplexNumber)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ComplexNumber} is of the form a+bi.
Description
- This function gives the exponential of a complex number.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMEXP(ComplexNumber)} , is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x+iy} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} &Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} are real numbers & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} is the imaginary unit. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt{-1}} .
- Euler's formula states that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ix}= cosx+isinx} , for any real number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e} is the base of the natural logarithm.
- The approximate value of the constant e=2.718281828459045 and it is equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^1} .
- Let z be the Complex Number.Then the exponential of a complex number is : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMEXP(z) = e^z = e^{x+iy} = e^{x}.e^{iy} = e^{x}.(cosy+isiny)=e^x.cosy+ie^x.siny} .
- Here Sin and Cos are trignometric functions. y is angle value in radians.
- When imaginary part is '0', it will give the exponent value of the real number. i.e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMEXP(z) = EXP(z)} when imaginary number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle iy} is '0'.
- The Complex exponential function is denoted by "cis(x)"(Cosine plus iSine)
- We can use COMPLEX function to convert the real and imaginary coefficients to a complex number.
Examples
- =IMEXP("2+3i") = -7.315110094901102+1.0427436562359i
- =IMEXP("4-5i") = 15.4874305606508+52.355491418482i
- =IMEXP("6") = 403.428793492735
- =IMEXP("2i") = -0.416146836547142+0.909297426825682i
- =IMEXP("0") = 1 and IMEXP("0i") = 1
ZOS Section
- The syntax is to calculate IMEXP in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMEXP(ComplexNumber)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ComplexNumber} is of the form a+bi.
- For e.g.,
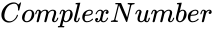 is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x+iy}
, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
&Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y}
are real numbers & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i}
is the imaginary unit. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt{-1}}
.
is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x+iy}
, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
&Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y}
are real numbers & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i}
is the imaginary unit. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt{-1}}
.