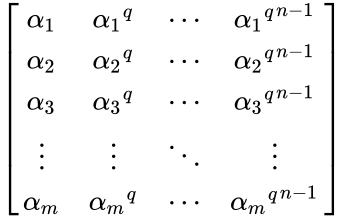Difference between revisions of "Manuals/calci/MOORE"
Jump to navigation
Jump to search
| Line 8: | Line 8: | ||
*But it is unrelated to the Moore determinant of a quaternionic Hermitian matrix. | *But it is unrelated to the Moore determinant of a quaternionic Hermitian matrix. | ||
*The Moore matrix has successive powers of the applied to the first column, so it is an mxn matrix of the form: | *The Moore matrix has successive powers of the applied to the first column, so it is an mxn matrix of the form: | ||
| − | <math>\begin{bmatrix} | + | <math> |
| − | \alpha_1 & {\alpha_1}^q &\cdots & {\alpha_1}^q^{n-1} \\ | + | \begin{bmatrix} |
| − | \alpha_2 & {\alpha_2}^q &\cdots & {\alpha_2}^q^{n-1} \\ | + | \alpha_1 & {\alpha_1}^q & \cdots & {{\alpha_1}^q}^{n-1} \\ |
| − | \alpha_3 & {\alpha_3}^q &\cdots & {\alpha_3}^q^{n-1} \\ | + | \alpha_2 & {\alpha_2}^q & \cdots & {{\alpha_2}^q}^{n-1} \\ |
| − | \vdots & \ddots & \vdots \\ | + | \alpha_3 & {\alpha_3}^q & \cdots & {{\alpha_3}^q}^{n-1} \\ |
| − | \alpha_m & {\alpha_m}^q &\cdots & {\alpha_m}^q^{n-1} \\ | + | \vdots & \vdots & \ddots & \vdots\\ |
| − | \end{bmatrix} </math> | + | \alpha_m & {\alpha_m}^q & \cdots & {{\alpha_m}^q}^{n-1} \\ |
| + | \end{bmatrix} | ||
| + | </math> | ||
*In calci, MATRIX("moore") is giving the matrixwith the element 1 of order 3. | *In calci, MATRIX("moore") is giving the matrixwith the element 1 of order 3. | ||
*And MATRIX("moore",4,1..4) is giving Moore matrix starting element 1 to 4 of order 4. | *And MATRIX("moore",4,1..4) is giving Moore matrix starting element 1 to 4 of order 4. | ||
Revision as of 03:42, 5 May 2015
MATRIX("MOORE",order)
- is the size of the Moore matrix.
Description
- This function gives the moore matrix of order 3 with the element 1.
- A moore matrix, is a square matrix over a finite field.
- When moore matrix is a square matrix, then its deteminant is called a Moore determinant.
- But it is unrelated to the Moore determinant of a quaternionic Hermitian matrix.
- The Moore matrix has successive powers of the applied to the first column, so it is an mxn matrix of the form:
- In calci, MATRIX("moore") is giving the matrixwith the element 1 of order 3.
- And MATRIX("moore",4,1..4) is giving Moore matrix starting element 1 to 4 of order 4.
Examples
- 1.MATRIX("moore")
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| 1 | 1 | 1 |
- 2.MATRIX("moore",5,1..5)
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 16 | 256 | 65536 |
| 3 | 9 | 81 | 6561 | 43046721 |
| 4 | 16 | 256 | 65536 | 4294967296 |
| 5 | 25 | 625 | 390625 | 152587890625 |
- 3.MATRIX("moore",4,3..7,"",2.3)
| 3 | 12.513502532843182 | 334.1730615222005 | 638460.9005874459 |
| 4 | 24.251465064166364 | 1530.7256306021752 | 21147737.669320222 |
| 5 | 40.51641491731905 | 4983.693475030862 | 319424366.94628483 |
| 6 | 61.623714938749366 | 13074.350231574774 | 2936069039.087338 |
See Also
 is the size of the Moore matrix.
is the size of the Moore matrix.