Difference between revisions of "Manuals/calci/PERMUTATION"
Jump to navigation
Jump to search
| Line 26: | Line 26: | ||
| 0 || 0 || 0 || 0 || 204 | | 0 || 0 || 0 || 0 || 204 | ||
|} | |} | ||
| − | *2.MATRIX("permutation",18) | + | *2.MATRIX("permutation",18).<math>\$</math>_(SUM) = 18 |
*3.MATRIX("permutation",5).<math>\$$$</math>(SUM)= | *3.MATRIX("permutation",5).<math>\$$$</math>(SUM)= | ||
{|class="wikitable" | {|class="wikitable" | ||
Latest revision as of 01:35, 26 October 2015
MATRIX("PERMUTATION",order)
- is the size of the Permutation matrix.
Description
- This function returns the matrix Permutation matrix of order 3.
- A permutation matrix is a square binary matrix obtained by permuting the rows of an nxn identity matrix according to some permutation of the numbers 1 to n.
- This matrix has exactly one entry 1 in each row and each column and 0's elsewhere.
- A permutation matrix is nonsingular, and its determiant + or -.
- Also permutation matrix A having the following properties , where is a transpose and I is the identity matrix.
- Permutation matrices are orthogonal .Hence, their inverse is their transpose: .
- A permutation matrix allows to exchange rows or columns of another via the matrix-matrix product.
- In calci MATRIX("permutation",4) gives the permutation matrix of order 4.
Examples
- 1.MATRIX("permutation",5,200..210)
| 0 | 0 | 0 | 200 | 0 |
| 0 | 201 | 0 | 0 | 0 |
| 202 | 0 | 0 | 0 | 0 |
| 0 | 0 | 203 | 0 | 0 |
| 0 | 0 | 0 | 0 | 204 |
- 2.MATRIX("permutation",18)._(SUM) = 18
- 3.MATRIX("permutation",5).(SUM)=
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
- 4.MATRIX("permutation",5).(SUM) =
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
 is the size of the Permutation matrix.
is the size of the Permutation matrix.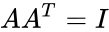 , where
, where 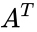 is a transpose and I is the identity matrix.
is a transpose and I is the identity matrix.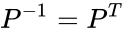 .
. _(SUM) = 18
_(SUM) = 18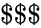 (SUM)=
(SUM)=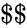 (SUM) =
(SUM) =