Difference between revisions of "Manuals/calci/BETADIST"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''BETADIST( | + | <div style="font-size:30px">'''BETADIST (Number,Alpha,Beta,LowerBound,UpperBound)'''</div><br/> |
| − | *<math> | + | *<math>Number</math> is the value between <math>LowerBound</math> and <math>UpperBound</math> |
| − | * | + | *<math>Alpha</math> and <math>Beta</math> are the value of the shape parameter |
| − | *<math> | + | *<math>LowerBound</math> & <math>UpperBound</math> the lower and upper limit to the interval of <math>x</math>. |
==Description== | ==Description== | ||
| Line 8: | Line 8: | ||
*The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by <math>\alpha</math> and <math>\beta</math>. | *The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by <math>\alpha</math> and <math>\beta</math>. | ||
*The Beta Distribution is also known as the Beta Distribution of the first kind. | *The Beta Distribution is also known as the Beta Distribution of the first kind. | ||
| − | *In <math> | + | *In <math>(Number,Alpha,Beta,LowerBound,UpperBound)</math>, <math>Number</math> is the value between <math>LowerBound</math> and <math>UpperBound</math>. |
| − | * | + | *Alpha is the value of the shape parameter. |
| − | * | + | *Beta is the value of the shape parameter |
| − | *<math> | + | *<math>LowerBound</math> and <math>UpperBound</math>(optional) are the Lower and Upper limit to the interval of <math>Number</math>. |
| − | *Normally <math> | + | *Normally <math>Number</math> lies between the limit <math>LowerBound</math> and <math>UpperBound</math>, suppose when we are omitting <math>a</math> and <math>b</math> value, by default <math>x</math> value with in 0 and 1. |
*The Probability Density Function of the beta distribution is: | *The Probability Density Function of the beta distribution is: | ||
<math>f(x)=\frac{x^{\alpha-1}(1-x)^{ \beta-1}}{B(\alpha,\beta)},</math> where <math>0 \le x \le 1</math>; <math>\alpha,\beta >0 </math> and <math>B(\alpha,\beta)</math> is the Beta function. | <math>f(x)=\frac{x^{\alpha-1}(1-x)^{ \beta-1}}{B(\alpha,\beta)},</math> where <math>0 \le x \le 1</math>; <math>\alpha,\beta >0 </math> and <math>B(\alpha,\beta)</math> is the Beta function. | ||
| Line 19: | Line 19: | ||
*This function will give the result as error when | *This function will give the result as error when | ||
1.Any one of the arguments are non-numeric. | 1.Any one of the arguments are non-numeric. | ||
| − | 2.<math> | + | 2.<math>Alpha \le 0</math> or <math>Beta \le 0</math> |
| − | 3.<math> | + | 3.<math>Number<LowerBound</math> ,<math>Number>UpperBound</math>, or <math>LowerBound=UpperBound</math> |
| − | *we are not mentioning the limit values <math> | + | *we are not mentioning the limit values <math>LowerBound</math> and <math>UpperBound</math>, |
| − | *By default it will consider the Standard Cumulative Beta Distribution, | + | *By default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1. |
==ZOS== | ==ZOS== | ||
Revision as of 16:14, 12 June 2018
BETADIST (Number,Alpha,Beta,LowerBound,UpperBound)
- is the value between and
- and are the value of the shape parameter
- & the lower and upper limit to the interval of .
Description
- This function gives the Cumulative Beta Probability Density function.
- The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by and .
- The Beta Distribution is also known as the Beta Distribution of the first kind.
- In , is the value between and .
- Alpha is the value of the shape parameter.
- Beta is the value of the shape parameter
- and (optional) are the Lower and Upper limit to the interval of .
- Normally lies between the limit and , suppose when we are omitting and value, by default value with in 0 and 1.
- The Probability Density Function of the beta distribution is:
where ; and is the Beta function.
- The formula for the Cumulative Beta Distribution is called the Incomplete Beta function ratio and it is denoted by and is defined as :
=, where ; and is the Beta function.
- This function will give the result as error when
1.Any one of the arguments are non-numeric. 2. or 3. ,, or
- we are not mentioning the limit values and ,
- By default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1.
ZOS
- The syntax is to calculate BEATDIST in ZOS is .
- is the value between LowerBound and UpperBound
- and are the value of the shape parameter.
- For e.g.,BETADIST(11..13,3,5,8,14)
- BETADIST(33..35,5..6,10..11,30,40)
Examples
- =BETADIST(0.4,8,10) = 0.35949234293309396
- =BETADIST(3,5,9,2,6) = 0.20603810250759128
- =BETADIST(9,4,2,8,11) = 0.04526748971193415
- =BETADIST(5,-1,-2,4,7) = #ERROR
Related Videos
See Also
References
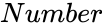 is the value between
is the value between  and
and 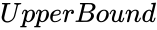
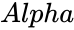 and
and 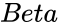 are the value of the shape parameter
are the value of the shape parameter .
.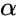 and
and 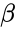 .
.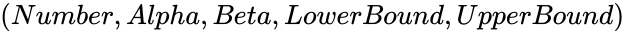 ,
,  and
and  value, by default
value, by default 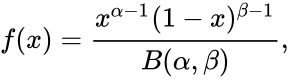 where
where  ;
; 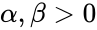 and
and 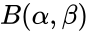 is the Beta function.
is the Beta function.
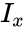 and is defined as :
and is defined as :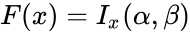 =
=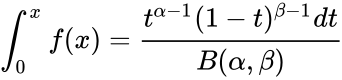 , where
, where 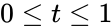 ;
;  or
or 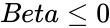 3.
3. ,
,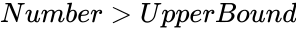 , or
, or 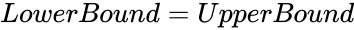
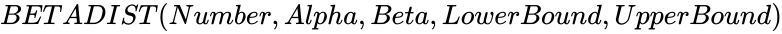 .
.
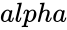 and
and  are the value of the shape parameter.
are the value of the shape parameter.