Difference between revisions of "Manuals/calci/IMCSCH"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''IMCSCH( | + | <div style="font-size:30px">'''IMCSCH(ComplexNumber)'''</div><br/> |
| − | * where | + | * where <math>ComplexNumber</math> is any complex number. |
==Description== | ==Description== | ||
*This function gives the hyperbolic cosec (csch) value of a complex number. | *This function gives the hyperbolic cosec (csch) value of a complex number. | ||
| − | * | + | *Consider the complex number in the form of <math>x+iy</math> |
*x & y are the real numbers. | *x & y are the real numbers. | ||
*'i' is the imaginary unit <math>i=\sqrt{-1}</math> | *'i' is the imaginary unit <math>i=\sqrt{-1}</math> | ||
| Line 13: | Line 13: | ||
== Examples == | == Examples == | ||
| − | '''IMCSCH( | + | '''IMCSCH(ComplexNumber)''' |
| − | *''' | + | *'''ComplexNumber''' is any complex number. |
{|id="TABLE1" class="SpreadSheet blue" | {|id="TABLE1" class="SpreadSheet blue" | ||
|- class="even" | |- class="even" | ||
| − | |'''IMCSCH( | + | |'''IMCSCH(ComplexNumber)''' |
|'''Value''' | |'''Value''' | ||
Revision as of 15:18, 16 July 2018
IMCSCH(ComplexNumber)
- where is any complex number.
Description
- This function gives the hyperbolic cosec (csch) value of a complex number.
- Consider the complex number in the form of
- x & y are the real numbers.
- 'i' is the imaginary unit
- Also x is called the real part & y is the imaginary part of a complex number.
- COMPLEX is the function used to convert Real & Imaginary numbers in to a complex number.
- is defined by
Examples
IMCSCH(ComplexNumber)
- ComplexNumber is any complex number.
| IMCSCH(ComplexNumber) | Value |
| IMCSCH("7+4i") | -0.001192090379815322+i0.0013802299076340766 |
| IMCSCH("7-8i") | -0.0002653570703635442+ⅈ0.001804354511817408 |
| IMCSCH("3") | 0.09982156966882273+i0 |
Related Videos
See Also
References
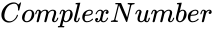 is any complex number.
is any complex number.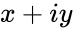
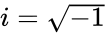
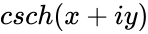 is defined by
is defined by