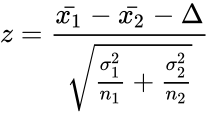Difference between revisions of "Manuals/calci/ZTESTTWOSAMPLEFORMEANS"
| Line 5: | Line 5: | ||
*<math>Alpha</math> is the significance level. | *<math>Alpha</math> is the significance level. | ||
*<math>NewTableFlag</math> is the logical value. | *<math>NewTableFlag</math> is the logical value. | ||
| + | **ZTESTTWOSAMPLEFORMEANS(), returns the logical value FALSE. | ||
==Description== | ==Description== | ||
Revision as of 16:33, 10 August 2018
- and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2} are array of values.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KnownVariance1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KnownVariance2} are value of variances.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle HypothesizedMeanDifference} is the Hypothesized Mean Difference.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Alpha} is the significance level.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NewTableFlag}
is the logical value.
- ZTESTTWOSAMPLEFORMEANS(), returns the logical value FALSE.
Description
- This function gives the z-test two sample for means.
- We can use this test when
1.The samples can be different sizes. 2.The two samples are independent. 3.Both populations are normally distributed or both sample sizes are large enough that the means are normally distributed.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ZTESTTWOSAMPLEFORMEANS(Array1,Array2,KnownVariance1,KnownVariance2,HypothesizedMeanDifference,Alpha,NewTableFlag)} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array1 } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2} are the set of values,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KnownVariance1} is the variance of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array1} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KnownVariance2} is the variance of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle HypothesizedMeanDifference } is the Hypothesized Mean Difference. If testing is for equal means,then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Hypothesized mean difference = 0} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Alpha} is the significance level which ranges from 0 to 1.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NewTableFlag} is the logical value like TRUE or FALSE.TRUE is indicating the result will display in new worksheet.
- Suppose we are omitted the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle lv} value it will consider the value as FALSE.
- ZTEST two sample for means is calculated by:
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{x_1}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{x_2}} are average of two samples, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} is the Hypothesized Mean Difference between two means of the population. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_2} are the standard deviation of two population. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_2} are the sizes of the samples.
- This function will give the result as error when
1. any one of the argument is nonnumeric. 2. Alpha>1
Examples
- Example 1
| A | B | |
|---|---|---|
| 1 | 70.25 | 90.02 |
| 2 | 82.87 | 89.45 |
| 3 | 90.17 | 70.89 |
| 4 | 45.55 | 107.91 |
| 5 | 51.98 | 59.09 |
| 6 | 21.28 | 45.03 |
| 7 | 39.04 | 56.08 |
| 8 | 40.47 | 91 |
| 9 | 30.02 | 40.41 |
| 10 | 100.05 | 29.04 |
| 11 | 86.1 | 37.79 |
| 12 | 72.49 | 41.07 |
| 13 | 29.54 | 52.04 |
| 14 | 38.76 | 60.78 |
| 15 | 47.01 | 66.06 |
| 16 | 50.65 | 78.01 |
| 17 | 55.91 | 41.22 |
| 18 | 102.7 | 33.99 |
| 19 | 10 | 110.02 |
- =ZTESTTWOSAMPLEFORMEANS(A1:A18,B1:B19,641.8474654,630.283176,0,0.5)
| VARIABLE1 | VARIABLE2 | |
|---|---|---|
| MEAN | 56.04421052631579 | 63.152631578947364 |
| KNOWN VARIANCE | 641.8474654 | 630.283176 |
| OBSERVATIONS | 19 | 19 |
| HYPOTHESIZED MEAN DIFFERENCE | 0 | |
| z VALUE | -0.8687285374505475 | |
| P(T<=+t) ONE-TAIL | 0.1924981032229391 | |
| z CRITICAL ONE-TAIL | 0 | |
| P(T<=t) TWO-TAIL | 0.3849962064458782 | |
| z CRITICAL TWO-TAIL | 0.6744897501960817 |
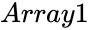 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2}
are array of values.
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2}
are array of values.